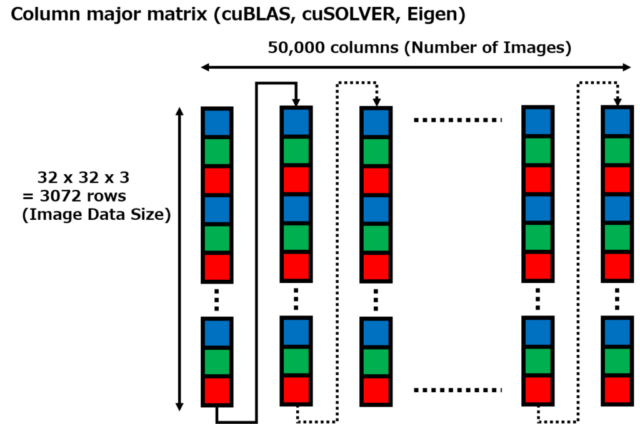Principal component analysis of Cifar10/Cifar100 image dataset in C# (using CUDA)
1. Overview
I wrote a C# program for principal component analysis of the Cifar10/Cifar100 image data set and wrote a description on this page before.
The above program required about 2 hours for principal component analysis of 50,000 image data (3,072 RGB values). The program was run on a Lifebook WU2/D2 laptop (model FMVWD2U27). When this principal component analysis was computed with Eigen in C++, the computation time was reduced to approximately 2 minutes and 30 seconds. I also checked the computation time on an ESPRIMO WD2/H2 desktop computer and found that the computation time for principal component analysis using Eigen in C++ was about 2 minutes. I prepared a page explaining this here.
This time, the principal component analysis calculation was rewritten in CUDA and performed on a GPGPU. Calculations were performed using an NVIDIA GeForce GTX 1650 on an ESPRIMO WD2/H2 desktop computer and confirmed that calculation time was reduced to approximately 12 seconds.
The source code for the CUDA version has been placed in the following GitHub repository.
https://github.com/fukagai-takuya/cifar10-cifar100-principal-component-analysis-with-cuda
2. Implementation
2.1. Installation of CUDA Toolkit 12.4
I downloaded Windows version of CUDA Toolkit 12.4 from the following page and installed it on a Windows 11 desktop computer, ESPRIMO WD2/H2.
https://developer.nvidia.com/cuda-downloads
2.2. Configure a DLL to use CUDA
I have rewritten the DLL portion of the Visual Studio 2022 solution here for a WPF application that displays Cifar10/Cifar100 image datasets in C# and performs principal component analysis with a DLL using C++ Eigen to CUDA implementation. For comparison of computation time, I also left the code of principal component analysis using Eigen in C++.
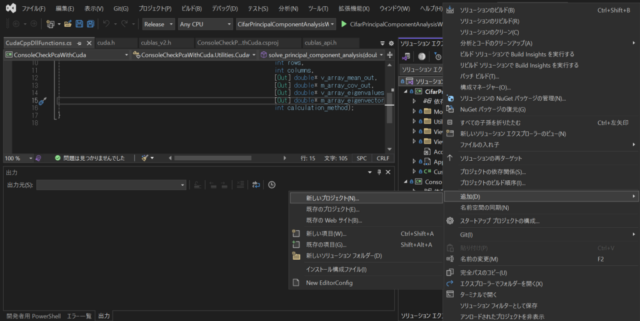
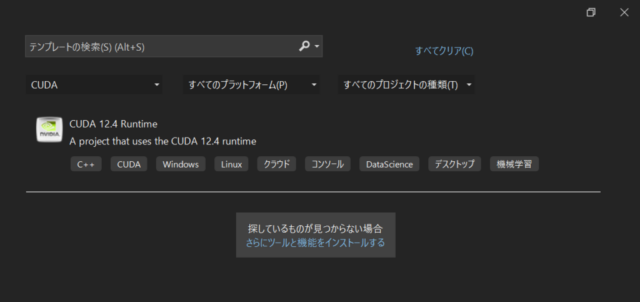
After deleting the project of building DLL using C++ Eigen, a new project was added to the solution as shown in the image below left. For the project to be added, I selected CUDA 12.4 Runtime as shown in the lower center image.
The project name is PrincipalComponentAnalysisWithCuda, as shown in the lower right image.
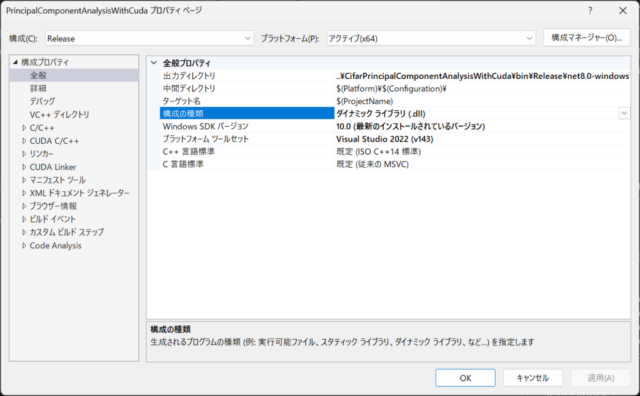
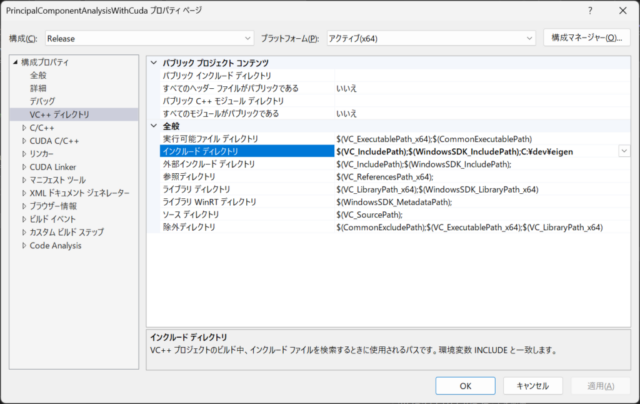
Since the CUDA 12.4 Runtime is a console application, I changed the property configuration type to Dynamic Library (.dll) as shown in the lower left image. Also, the output directory of the DLL was changed to the directory where the C# project executable (.exe) is output.
Since I also added a function for principal component analysis using C++ Eigen in the DLL, I added the Eigen installation directory C:\dev\eigen to the include directory, as shown in the lower center image.
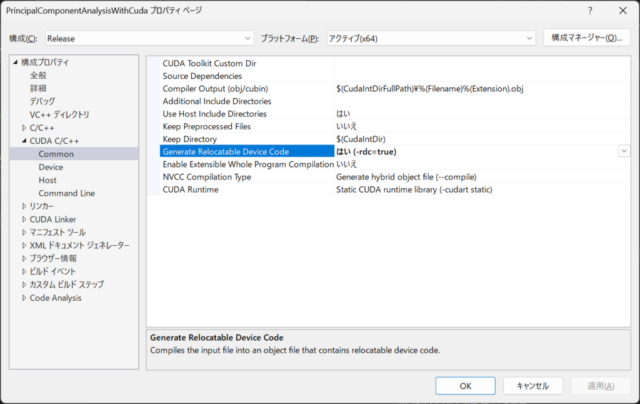
Since I prepared the file that uses CUDA with extension .cu and the file that uses Eigen with extension .cpp, I selected -rdc=true in the CUDA C/C++ settings as shown in the image below right. (By selecting -rdc=true, a DLL consisting of multiple files including .cu file will be built.)
When the code using Eigen was written in a file with extension .cu, the processing time for principal component analysis using Eigen became longer, so it was split as described above. After splitting the file and creating a single DLL, the processing time for principal component analysis using Eigen is about the same as the processing time described on this page.
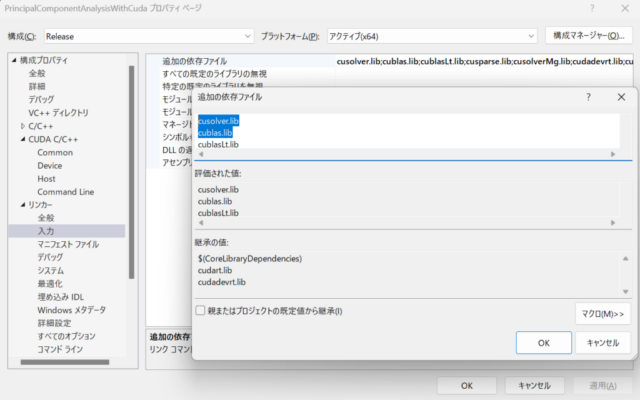
To use the cuBLAS and cuSOLVER libraries, I added cusolver.lib and cublas.lib to the additional dependency files in the linker input as shown in the first image below.
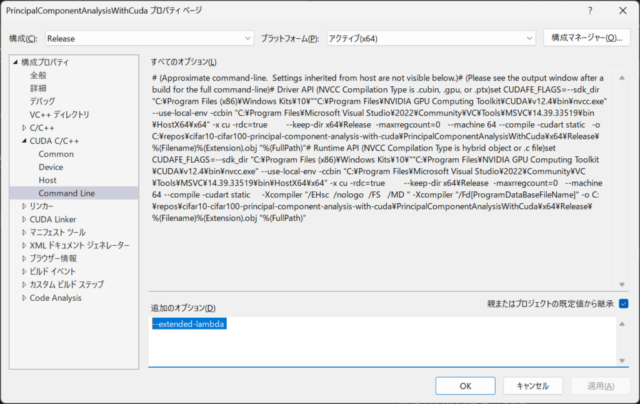
To use code that utilizes lambda expressions, I added the –extended-lambda command line option for CUDA C/C++ as shown in the second image below.
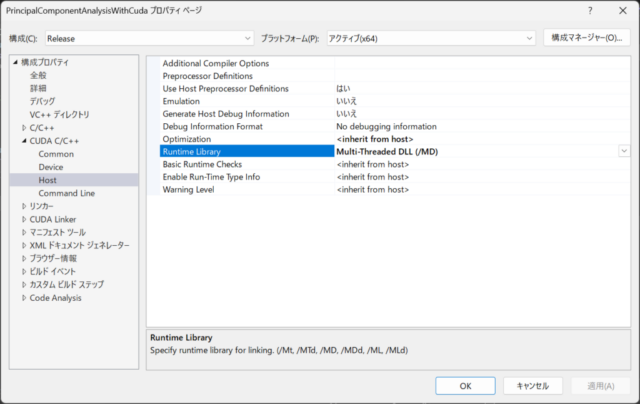
Multi-Threaded DLL (/MD) is now selected as the host-side Runtime Library for CUDA C/C++ as shown in the third image below.
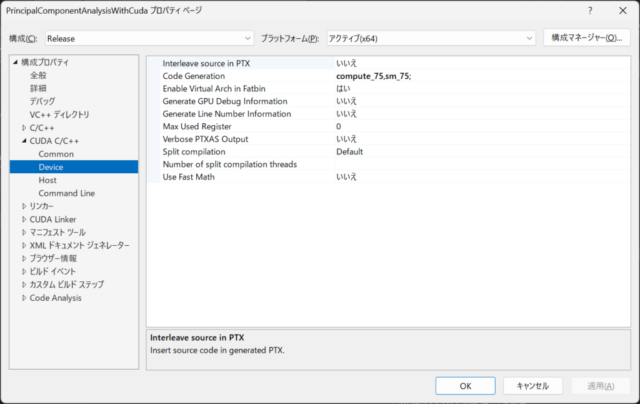
As shown in the fourth image below, I specified compute_75,sm_75; as Code Generation for the CUDA C/C++ Device, corresponding to the GPGPU, NVIDIA GeForce GTX 1650.
This solution also includes a project called ConsoleCheckPcaWithCuda in C#. This is a project for a console program prepared for a simple check of calculations with a CUDA-implemented DLL.
2.3. Calculation of Principal Component Analysis with DLL in C++ (common part of calculations using CUDA and Eigen)
The following four files have been added to the DLL project to perform principal component analysis with CUDA and Eigen.
- PrincipalComponentAnalysis.h
- PrincipalComponentAnalysis.cpp
- PrincipalComponentAnalysisWithCuda.cu
- PrincipalComponentAnalysisWithEigen.cpp
PrincipalComponentAnalysis.h is a header file that looks like the following.
The C# program receives a parameter indicating whether the principal component analysis calculation is to be performed by CUDA or Eigen, and depending on the parameter, one of the two functions listed in the header file is executed.
The __ENABLE_CONSOLE_TEST_CODES__ switches between outputting the progress and results of a principal component analysis calculation to the console. It includes calculations to check the results of the eigenvalue decomposition, and the execution time varies depending on whether __ENABLE_CONSOLE_TEST_CODES__ is enabled or not. I disabled __ENABLE_CONSOLE_TEST_CODES__ when evaluating computation time, as shown in the code below.
#pragma once
#define DLLEXPORT extern "C" __declspec(dllexport)
//#define __ENABLE_CONSOLE_TEST_CODES__
#include <iostream>
#include <vector>
#include <cuda_runtime.h>
#include <cublas_v2.h>
#include <cusolverDn.h>
#include <library_types.h>
#include <thrust/device_vector.h>
#include <thrust/reverse.h>
#include <thrust/for_each.h>
#include <Eigen/Core>
#include <Eigen/Eigenvalues>
/**
* Calculate Principal Component Analysis with Eigen (C++ implementation)
*
* - Since Eigen matrix is column-major, m_array_input's rows and columns are swapped from C# interface
*
* @param m_array_input Pointer to an input matrix values (length: rows * columns): column-major matrix (M_input)
* @param columns Number of columns of an input matrix: Number of sample vectors
* @param rows Number of rows of an input matrix: Size of sample vector
* @param v_array_mean_out Pointer to an output mean vector (length: rows): Mean of sample vectors
* @param m_array_cov_out Pointer to an output covariance martix (length: rows * rows): Covariance matrix of sample vectors
* @param v_array_eigenvalues_out Pointer to an output eigenvalues vector (length: rows): Eigenvalues of covariance matrix
* @param m_array_eigenvectors_out Pointer to an output eigenvectors martix (length: rows * rows): Eigenvectors of covariance matrix (row-major)
*/
void solve_principal_component_analysis_with_eigen(double* m_array_input,
const int columns,
const int rows,
double* v_array_mean_out,
double* m_array_cov_out,
double* v_array_eigenvalues_out,
double* m_array_eigenvectors_out);
/**
* Calculate Principal Component Analysis with cuBLAS and cuSOLVER (CUDA implementation)
*
* - Since cuBLAS and cuSOLVER matrix is column-major, m_array_input's rows and columns are swapped from C# interface
*
* @param m_array_input Pointer to an input matrix values (length: rows * columns): column-major matrix (M_input)
* @param columns Number of columns of an input matrix: Number of sample vectors
* @param rows Number of rows of an input matrix: Size of sample vector
* @param v_array_mean_out Pointer to an output mean vector (length: rows): Mean of sample vectors
* @param m_array_cov_out Pointer to an output covariance martix (length: rows * rows): Covariance matrix of sample vectors
* @param v_array_eigenvalues_out Pointer to an output eigenvalues vector (length: rows): Eigenvalues of covariance matrix
* @param m_array_eigenvectors_out Pointer to an output eigenvectors martix (length: rows * rows): Eigenvectors of covariance matrix (row-major)
*/
void solve_principal_component_analysis_with_cuda(const double* m_array_input,
const int columns,
const int rows,
double* v_array_mean_out,
double* m_array_cov_out,
double* v_array_eigenvalues_out,
double* m_array_eigenvectors_out);
PrincipalComponentAnalysis.cpp is the following file. From the C# code, the function solve_principal_component_analysis in the following file is called. The last argument of the function, calculation_method, specifies whether to perform a principal component analysis using CUDA or C++ Eigen.
In order to be able to call it from C#, the DLLEXPORT described in the header file is prefixed to the function definition as DLLEXPORT void solve_principal_component_analysis.
#ifdef __ENABLE_CONSOLE_TEST_CODES__ to #endif is the code to check the results of the principal component analysis calculation, and outputs the calculated covariance matrix, the eigenvalues and eigenvectors of the covariance matrix sorted in descending order, and the results of checking the eigenvalue decomposition of the covariance matrix. M_cov in the console output is the covariance matrix, V is the matrix of eigenvectors ordered from the first column, Vt is the transpose matrix of V, and L is the diagonal matrix of eigenvalues arranged as diagonal components.
#include "PrincipalComponentAnalysis.h"
using namespace std;
using namespace Eigen;
/**
* Specify calculation method
* - Use Eigen for the Calculation of Principal Component Analysis
*/
const int CALCULATE_WITH_EIGEN = 0;
/**
* Specify calculation method
* - Use CUDA for the Calculation of Principal Component Analysis
*/
const int CALCULATE_WITH_CUDA = 1;
/**
* Calculate Principal Component Analysis
*
* - Since Eigen, cuBLAS and cuSOLVER matrix is column-major, m_array_input's rows and columns are swapped from C# interface
*
* @param m_array_input Pointer to an input matrix values (length: rows * columns): column-major matrix
* @param columns Number of columns of an input matrix: Number of sample vectors
* @param rows Number of rows of an input matrix: Size of sample vector
* @param v_array_mean_out Pointer to an output mean vector (length: rows): Mean of sample vectors
* @param m_array_cov_out Pointer to an output covariance martix (length: rows * rows): Covariance matrix of sample vectors
* @param v_array_eigenvalues_out Pointer to an output eigenvalues vector (length: rows): Eigenvalues of covariance matrix
* @param m_array_eigenvectors_out Pointer to an output eigenvectors martix (length: rows * rows): Eigenvectors of covariance matrix (row-major)
* @param calculation_method 0:Eigen, 1:CUDA
*/
DLLEXPORT void solve_principal_component_analysis(double* m_array_input,
const int columns,
const int rows,
double* v_array_mean_out,
double* m_array_cov_out,
double* v_array_eigenvalues_out,
double* m_array_eigenvectors_out,
const int calculation_method = CALCULATE_WITH_EIGEN)
{
cout << "--- C++ codes (START) ---" << endl;
cout << "--- solve_principal_component_analysis (START) ---" << endl;
if (calculation_method == CALCULATE_WITH_EIGEN) {
solve_principal_component_analysis_with_eigen(m_array_input,
columns,
rows,
v_array_mean_out,
m_array_cov_out,
v_array_eigenvalues_out,
m_array_eigenvectors_out);
} else if (calculation_method == CALCULATE_WITH_CUDA) {
solve_principal_component_analysis_with_cuda(m_array_input,
columns,
rows,
v_array_mean_out,
m_array_cov_out,
v_array_eigenvalues_out,
m_array_eigenvectors_out);
}
// ---------------------------------------------------------------
// Test codes (Start)
// ---------------------------------------------------------------
#ifdef __ENABLE_CONSOLE_TEST_CODES__
// Map m_array_cov_out to MatrixXd
// - The size of rows are the same as the input rows
// - Since m_array_cov_out stores values of a symmetric matrix,
// it is not affected by the difference between column-major and row-major.
Map<MatrixXd> M_cov(m_array_cov_out, rows, rows);
cout << "M_cov is prepared." << endl;
cout << M_cov(0, 0) << ", ..., " << M_cov(0, rows - 1) << endl;
cout << "..." << endl;
cout << M_cov(rows - 1, 0) << ", ..., " << M_cov(rows - 1, rows - 1) << endl << endl;
// Map v_array_eigenvalues_out to VectorXd
Map<VectorXd> eigenvalues(v_array_eigenvalues_out, rows);
cout << "eigenvalues" << endl;
cout << eigenvalues(0) << ", ..., " << eigenvalues(rows - 1) << endl << endl;
// Map m_array_eigenvectors_out to MatrixXd
// - Since m_array_eigenvectors_out is row-major map to row-major matrix
Map<Matrix<double, Dynamic, Dynamic, RowMajor>> eigenvectors(m_array_eigenvectors_out, rows, rows);
cout << "eigenvectors" << endl;
cout << eigenvectors(0, 0) << ", ..., " << eigenvectors(0, rows - 1) << endl;
cout << "..." << endl;
cout << eigenvectors(rows - 1, 0) << ", ..., " << eigenvectors(rows - 1, rows - 1) << endl << endl;
MatrixXd M_cov_V = M_cov * eigenvectors;
cout << "Check Result: M_cov * V" << endl;
cout << M_cov_V(0, 0) << ", ..., " << M_cov_V(0, rows - 1) << endl;
cout << "..." << endl;
cout << M_cov_V(rows - 1, 0) << ", ..., " << M_cov_V(rows - 1, rows - 1) << endl << endl;
MatrixXd V_L = eigenvectors * eigenvalues.asDiagonal();
cout << "Check Result: V * L" << endl;
cout << V_L(0, 0) << ", ..., " << V_L(0, rows - 1) << endl;
cout << "..." << endl;
cout << V_L(rows - 1, 0) << ", ..., " << V_L(rows - 1, rows - 1) << endl << endl;
MatrixXd VVt = eigenvectors * eigenvectors.transpose();
cout << "Check Result: V V^t" << endl;
cout << VVt(0, 0) << ", ..., " << VVt(0, rows - 1) << endl;
cout << "..." << endl;
cout << VVt(rows - 1, 0) << ", ..., " << VVt(rows - 1, rows - 1) << endl << endl;
MatrixXd VLVt = eigenvectors * eigenvalues.asDiagonal() * eigenvectors.transpose();
cout << "Check Result: V L V^t" << endl;
cout << VLVt(0, 0) << ", ..., " << VLVt(0, rows - 1) << endl;
cout << "..." << endl;
cout << VLVt(rows - 1, 0) << ", ..., " << VLVt(rows - 1, rows - 1) << endl << endl;
// ---------------------------------------------------------------
// Test codes (End)
// ---------------------------------------------------------------
#endif
cout << "--- solve_principal_component_analysis (END) ---" << endl;
cout << "--- C++ codes (END) ---" << endl;
}
2.4. Computing Principal Component Analysis with CUDA
PrincipalComponentAnalysisWithCuda.cu uses cuBLAS, cuSOLVER, and thrust to perform the principal component analysis calculation, as shown in the code below.
A calculation was performed in cublasDgemm to take the product of a 3,072-by-50,000 matrix and its transpose matrix to obtain a 3,072-by-3,072 covariance matrix. Compared to calculations using Eigen, the calculation time was significantly reduced.
The eigenvalue decomposition of the covariance matrix was computed with cusolverDnXsyevd in cuSOLVER, which performs eigenvalue decomposition of a symmetric matrix.
When input data was set to the array m_array_input on the C# side, 50,000 rows of image data consisting of 3,072 elements were set in each row of the two-dimensional array double[,]. Each row corresponds to the data of one image, and 50,000 image data were set. Because C#’s two-dimensional array double[,] places data in row major order, the one-dimensional array m_array_input has data set in the order of 3,072 elements in the first row, 3,072 elements in the second row, …, and 3,072 elements in the 50,000th row.
Since cuBLAS and cuSOLVER assume that matrix data is arranged in column major order, the calculation is performed assuming that the one-dimensional array m_array_input contains 3,072 rows and 50,000 columns of data. The second argument rows (number of rows) and the third argument columns (number of columns) of the function that calls solve_principal_component_analysis on the C# side are replaced in solve_principal_component_analysis_with_cuda, with columns as the second argument and rows as the third argument.
The eigenvalues obtained using cusolverDnXsyevd are arranged in ascending order, and the matrix of corresponding eigenvectors is also arranged in that order. The eigenvalues are rearranged in descending order, and the matrix of eigenvectors is rearranged accordingly. I use thrust::for_each for the calculation to sort the order of the eigenvector columns, and a lambda expression is used in this calculation. Therefore, I added –extended-lambda to the command line option when building the CUDA C/C++ DLL as shown above.
The C# code expects to receive the results of the calculation as row major, so the CUDA code below takes the transpose of the matrix of eigenvectors and then copies the values into the m_array_eigenvectors_out array.
#include "PrincipalComponentAnalysis.h"
// CUDA API error checking
#define CUDA_CHECK(err) \
do { \
cudaError_t err_ = (err); \
if (err_ != cudaSuccess) { \
std::printf("CUDA error %d at %s:%d\n", err_, __FILE__, __LINE__); \
throw std::runtime_error("CUDA error"); \
} \
} while (0)
// cublas API error checking
#define CUBLAS_CHECK(err) \
do { \
cublasStatus_t err_ = (err); \
if (err_ != CUBLAS_STATUS_SUCCESS) { \
std::printf("cublas error %d at %s:%d\n", err_, __FILE__, __LINE__); \
throw std::runtime_error("cublas error"); \
} \
} while (0)
// cusolver API error checking
#define CUSOLVER_CHECK(err) \
do { \
cusolverStatus_t err_ = (err); \
if (err_ != CUSOLVER_STATUS_SUCCESS) { \
std::printf("cusolver error %d at %s:%d\n", err_, __FILE__, __LINE__); \
throw std::runtime_error("cusolver error"); \
} \
} while (0)
template <typename T>
struct linear_index_to_row_index : public thrust::unary_function<T,T> {
T rows; // --- Number of rows
__host__ __device__ linear_index_to_row_index(T rows) : rows(rows) {}
__host__ __device__ T operator()(T i) { return i % rows; }
};
/**
* Calculate Principal Component Analysis with cuBLAS and cuSOLVER (CUDA implementation)
*
* - Since cuBLAS and cuSOLVER matrix is column-major, m_array_input's rows and columns are swapped from C# interface
*
* @param m_array_input Pointer to an input matrix values (length: rows * columns): column-major matrix (M_input)
* @param columns Number of columns of an input matrix: Number of sample vectors
* @param rows Number of rows of an input matrix: Size of sample vector
* @param v_array_mean_out Pointer to an output mean vector (length: rows): Mean of sample vectors
* @param m_array_cov_out Pointer to an output covariance martix (length: rows * rows): Covariance matrix of sample vectors
* @param v_array_eigenvalues_out Pointer to an output eigenvalues vector (length: rows): Eigenvalues of covariance matrix
* @param m_array_eigenvectors_out Pointer to an output eigenvectors martix (length: rows * rows): Eigenvectors of covariance matrix (row-major)
*/
void solve_principal_component_analysis_with_cuda(const double* m_array_input,
const int columns,
const int rows,
double* v_array_mean_out,
double* m_array_cov_out,
double* v_array_eigenvalues_out,
double* m_array_eigenvectors_out)
{
cublasHandle_t cublasH = NULL;
cudaStream_t stream = NULL;
// Create cublas handle, bind a stream
CUBLAS_CHECK(cublasCreate(&cublasH));
CUDA_CHECK(cudaStreamCreateWithFlags(&stream, cudaStreamNonBlocking));
CUBLAS_CHECK(cublasSetStream(cublasH, stream));
thrust::device_vector<double> d_M_input(rows * columns); // M_input
thrust::device_vector<double> d_V_ones(columns, 1.f); // V_ones = [1, ..., 1]^t
thrust::device_vector<double> d_V_mean(rows); // V_mean = 1 / columns * M_input * [1, ..., 1]^t
thrust::device_vector<double> d_M_cov(rows * rows); // M_cov = A * A^t (A = M_input - [V_mean, ..., V_mean])
thrust::device_vector<double> d_M_eingenvectors_row_major(rows * rows); // Eigenvectors of M_cov (row-major matrix)
CUDA_CHECK(cudaMemcpyAsync(thrust::raw_pointer_cast(d_M_input.data()), m_array_input, sizeof(double) * rows * columns,
cudaMemcpyHostToDevice, stream));
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "M_input: " << d_M_input[0] << ", ..., " << d_M_input[(columns - 1) * rows] << std::endl;
std::cout << "M_input: " << "......" << std::endl;
std::cout << "M_input: " << d_M_input[rows - 1] << ", ..., " << d_M_input[rows * columns - 1] << std::endl << std::endl;
#endif
// -------------------------------------------------------------------------------------------
// Calculation of Mean Vector: V_mean = 1 / columns * M_input * [1, ..., 1]^t
// -------------------------------------------------------------------------------------------
double alpha = 1.0 / columns;
double beta = 0.0;
CUBLAS_CHECK(cublasDgemv(cublasH, CUBLAS_OP_N, rows, columns, &alpha, thrust::raw_pointer_cast(d_M_input.data()), rows,
thrust::raw_pointer_cast(d_V_ones.data()), 1, &beta, thrust::raw_pointer_cast(d_V_mean.data()), 1));
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "V_mean: " << d_V_mean[0] << ", ..., " << d_V_mean[rows - 1] << std::endl << std::endl;
#endif
// -------------------------------------------------------------------------------------------
// Subtract mean colum vector from input Matrix columns: A = M_input - [V_mean, ..., V_mean]
// -------------------------------------------------------------------------------------------
thrust::transform(d_M_input.begin(), d_M_input.end(),
thrust::make_permutation_iterator(d_V_mean.begin(),
thrust::make_transform_iterator(thrust::make_counting_iterator(0),
linear_index_to_row_index<int>(rows))),
d_M_input.begin(),
thrust::minus<double>());
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "M_input - V_mean: " << d_M_input[0] << ", ..., " << d_M_input[(columns - 1) * rows] << std::endl;
std::cout << "M_input - V_mean: " << "......" << std::endl;
std::cout << "M_input - V_mean: " << d_M_input[rows - 1] << ", ..., " << d_M_input[rows * columns - 1] << std::endl << std::endl;
#endif
// -------------------------------------------------------------------------------------------
// Calculation of Covariance Matrix: M_cov = A * A^t (A = M_input - [V_mean, ..., V_mean])
// -------------------------------------------------------------------------------------------
alpha = 1.0;
beta = 0.0;
CUBLAS_CHECK(cublasDgemm(cublasH, CUBLAS_OP_N, CUBLAS_OP_T, rows, rows, columns, &alpha,
thrust::raw_pointer_cast(d_M_input.data()), rows,
thrust::raw_pointer_cast(d_M_input.data()), rows, &beta,
thrust::raw_pointer_cast(d_M_cov.data()), rows));
// Copy data to host
CUDA_CHECK(cudaMemcpyAsync(v_array_mean_out, thrust::raw_pointer_cast(d_V_mean.data()), sizeof(double) * rows,
cudaMemcpyDeviceToHost, stream));
CUDA_CHECK(cudaMemcpyAsync(m_array_cov_out, thrust::raw_pointer_cast(d_M_cov.data()), sizeof(double) * rows * rows,
cudaMemcpyDeviceToHost, stream));
CUDA_CHECK(cudaStreamSynchronize(stream));
// ---------------------------------------------------------------
// Eigendecomposition of a covariance matrix
// ---------------------------------------------------------------
cusolverDnHandle_t cusolverH = NULL;
cusolverDnParams_t params = NULL;
thrust::device_vector<double> d_V_eigenvalues(rows);
thrust::device_vector<int> d_info(1);
int info = 0;
size_t workspaceInBytesOnDevice = 0; // size of workspace
void *d_work = nullptr; // device workspace
size_t workspaceInBytesOnHost = 0; // size of workspace
void *h_work = nullptr; // host workspace
// Create cusolver handle, bind a stream
CUSOLVER_CHECK(cusolverDnCreate(&cusolverH));
CUSOLVER_CHECK(cusolverDnSetStream(cusolverH, stream));
CUSOLVER_CHECK(cusolverDnCreateParams(¶ms));
// Query working space of syevd
cusolverEigMode_t jobz = CUSOLVER_EIG_MODE_VECTOR; // Compute eigenvalues and eigenvectors
cublasFillMode_t uplo = CUBLAS_FILL_MODE_LOWER; // Lower triangle of d_M_cov is stored
CUSOLVER_CHECK(cusolverDnXsyevd_bufferSize(cusolverH, params, jobz, uplo, rows, CUDA_R_64F, thrust::raw_pointer_cast(d_M_cov.data()), rows,
CUDA_R_64F, thrust::raw_pointer_cast(d_V_eigenvalues.data()), CUDA_R_64F,
&workspaceInBytesOnDevice, &workspaceInBytesOnHost));
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::printf("cusolverDnXsyevd_bufferSize: workspaceInBytesOnDevice = %zu\n", workspaceInBytesOnDevice);
std::printf("cusolverDnXsyevd_bufferSize: workspaceInBytesOnHost = %zu\n", workspaceInBytesOnHost);
#endif
CUDA_CHECK(cudaMalloc(reinterpret_cast<void **>(&d_work), workspaceInBytesOnDevice));
if (workspaceInBytesOnHost > 0) {
h_work = reinterpret_cast<void *>(malloc(workspaceInBytesOnHost));
if (h_work == nullptr) {
throw std::runtime_error("Error: h_work not allocated.");
}
}
// Compute eigendecomposition
CUSOLVER_CHECK(cusolverDnXsyevd(cusolverH, params, jobz, uplo, rows, CUDA_R_64F,
thrust::raw_pointer_cast(d_M_cov.data()), rows, CUDA_R_64F,
thrust::raw_pointer_cast(d_V_eigenvalues.data()), CUDA_R_64F, d_work, workspaceInBytesOnDevice,
h_work, workspaceInBytesOnHost, thrust::raw_pointer_cast(d_info.data())));
// Apply thrust::reverse() to make the order of eigenvalues decreasing order
thrust::reverse(d_V_eigenvalues.begin(), d_V_eigenvalues.end());
// Since the order of eigenvalues is reversed,
// reverse the column order of eigenvectors matrix (column-major matrix)
int m_eigenvectors_size = rows * rows;
int m_eigenvectors_rows = rows;
int m_eigenvectors_columns = rows;
double *d_M_eigenvectors_ptr = (double *)thrust::raw_pointer_cast(d_M_cov.data());
auto counting = thrust::make_counting_iterator<int>(0);
thrust::for_each(thrust::cuda::par.on(stream), counting,
counting + (m_eigenvectors_size / 2), [=] __device__(int idx) {
int dest_row = idx % m_eigenvectors_rows;
int dest_col = idx / m_eigenvectors_rows;
int src_row = dest_row;
int src_col = (m_eigenvectors_columns - dest_col) - 1;
int src_idx = src_col * m_eigenvectors_rows + src_row;
double temp = d_M_eigenvectors_ptr[idx];
d_M_eigenvectors_ptr[idx] = d_M_eigenvectors_ptr[src_idx];
d_M_eigenvectors_ptr[src_idx] = temp;
});
// Make the order of eigenvectors matrix (column-major matrix) row-major matrix : Transpose
alpha = 1.0;
beta = 0.0;
CUBLAS_CHECK(cublasDgeam(cublasH, CUBLAS_OP_T, CUBLAS_OP_N, rows, rows, &alpha,
d_M_eigenvectors_ptr, rows, &beta,
d_M_eigenvectors_ptr, rows,
thrust::raw_pointer_cast(d_M_eingenvectors_row_major.data()), rows));
CUDA_CHECK(cudaMemcpyAsync(m_array_eigenvectors_out, thrust::raw_pointer_cast(d_M_eingenvectors_row_major.data()),
sizeof(double) * rows * rows,
cudaMemcpyDeviceToHost, stream));
CUDA_CHECK(cudaMemcpyAsync(v_array_eigenvalues_out, thrust::raw_pointer_cast(d_V_eigenvalues.data()), sizeof(double) * rows,
cudaMemcpyDeviceToHost, stream));
CUDA_CHECK(cudaMemcpyAsync(&info, thrust::raw_pointer_cast(d_info.data()), sizeof(int), cudaMemcpyDeviceToHost, stream));
CUDA_CHECK(cudaStreamSynchronize(stream));
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::printf("after Xsyevd: info = %d\n", info);
#endif
if (0 > info) {
std::printf("%d-th parameter is wrong \n", -info);
exit(1);
}
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::printf("\n\n");
#endif
// free resources
CUDA_CHECK(cudaFree(d_work));
free(h_work);
CUBLAS_CHECK(cublasDestroy(cublasH));
CUSOLVER_CHECK(cusolverDnDestroy(cusolverH));
CUDA_CHECK(cudaStreamDestroy(stream));
}
2.5. Computing Principal Component Analysis with Eigen
PrincipalComponentAnalysisWithEigen.cpp uses Eigen to perform principal component analysis calculations, as shown in the code below.
It is almost the same as the code for principal component analysis using Eigen on this page.
Since Eigen matrices are column major by default, as in the CUDA code, the data set in the row major 50,000 rows, 3,072 columns two-dimensional array double[,] on the C# side is swapped between rows and columns and treated as a column major 3,072 rows, 50,000 columns array.
Unlike the code for principal component analysis using Eigen on this page, the only matrix prepared on the Eigen side as a row major matrix is the matrix that stores the eigenvectors obtained by eigenvalue decomposition of the covariance matrix.
#include "PrincipalComponentAnalysis.h"
using namespace std;
using namespace Eigen;
/**
* Calculate Principal Component Analysis with Eigen (C++ implementation)
*
* - Since Eigen matrix is column-major, m_array_input's rows and columns are swapped from C# interface
*
* @param m_array_input Pointer to an input matrix values (length: rows * columns): column-major matrix (M_input)
* @param columns Number of columns of an input matrix: Number of sample vectors
* @param rows Number of rows of an input matrix: Size of sample vector
* @param v_array_mean_out Pointer to an output mean vector (length: rows): Mean of sample vectors
* @param m_array_cov_out Pointer to an output covariance martix (length: rows * rows): Covariance matrix of sample vectors
* @param v_array_eigenvalues_out Pointer to an output eigenvalues vector (length: rows): Eigenvalues of covariance matrix
* @param m_array_eigenvectors_out Pointer to an output eigenvectors martix (length: rows * rows): Eigenvectors of covariance matrix (row-major)
*/
void solve_principal_component_analysis_with_eigen(double* m_array_input,
const int columns,
const int rows,
double* v_array_mean_out,
double* m_array_cov_out,
double* v_array_eigenvalues_out,
double* m_array_eigenvectors_out)
{
// Map m_array_input to MatrixXd
// - Since Eigen matrix is column-major, rows and columns are swapped from C# interface
// - M_input (column-major) is a transposed matrix of C# m_array_input matrix (row-major)
Map<MatrixXd> M_input(m_array_input, rows, columns);
// Map v_array_mean_out to VectorXd
Map<VectorXd> V_mean(v_array_mean_out, rows);
// Map m_array_cov_out to MatrixXd
Map<MatrixXd> M_cov(m_array_cov_out, rows, rows);
// Map v_array_eigenvalues_out to VectorXd
Map<VectorXd> eigenvalues(v_array_eigenvalues_out, rows);
// Map m_array_eigenvectors_out to MatrixXd
// - Since map m_array_cov_out is row-major, map as a row-major matrix
Map<Matrix<double, Dynamic, Dynamic, RowMajor>> eigenvectors(m_array_eigenvectors_out, rows, rows);
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "M_input is prepared." << std::endl;
std::cout << M_input(0, 0) << ", ..., " << M_input(0, columns - 1) << std::endl;
std::cout << "......" << std::endl;
std::cout << M_input(rows - 1, 0) << ", ..., " << M_input(rows - 1, columns - 1) << std::endl << std::endl;
#endif
// Calculate the mean of sample row vectors
V_mean = M_input.rowwise().mean();
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "V_mean is prepared." << std::endl;
std::cout << V_mean(0) << ", ..., " << V_mean(rows - 1) << std::endl << std::endl;
#endif
// Subtract v_mean.transpose() from each sample row vector
M_input = M_input.colwise() - V_mean;
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "M_input - V_mean is prepared." << std::endl;
std::cout << M_input(0, 0) << ", ..., " << M_input(0, columns - 1) << std::endl;
std::cout << "......" << std::endl;
std::cout << M_input(rows - 1, 0) << ", ..., " << M_input(rows - 1, columns - 1) << std::endl << std::endl;
#endif
// Calculate covariance matrix
// - Ignore the effect of constant multiplication
// - Skip division by N or N - 1 (N is sample size)
M_cov = M_input * M_input.transpose();
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "M_cov is prepared." << std::endl;
std::cout << M_cov(0, 0) << ", ..., " << M_cov(0, rows - 1) << std::endl;
std::cout << "..." << endl;
std::cout << M_cov(rows - 1, 0) << ", ..., " << M_cov(rows - 1, rows - 1) << std::endl << std::endl;
#endif
// ---------------------------------------------------------------
// Calculate the Eigendecomposition of a covariance matrix
// ---------------------------------------------------------------
SelfAdjointEigenSolver<MatrixXd> esolver(M_cov);
eigenvalues = esolver.eigenvalues();
eigenvectors = esolver.eigenvectors();
// Apply reverse() to make the order of eigenvalues decreasing order
eigenvalues = eigenvalues.reverse().eval();
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "eigenvalues" << std::endl;
std::cout << eigenvalues(0) << ", ..., " << eigenvalues(rows - 1) << std::endl << std::endl;
#endif
// Apply reverse() to eigenvectors because the order of eigenvalues are reversed
eigenvectors = eigenvectors.rowwise().reverse().eval();
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "eigenvectors" << endl;
std::cout << eigenvectors(0, 0) << ", ..., " << eigenvectors(0, rows - 1) << std::endl;
std::cout << "..." << endl;
std::cout << eigenvectors(rows - 1, 0) << ", ..., " << eigenvectors(rows - 1, rows - 1) << std::endl << std::endl;
#endif
}
2.6. C# code that calls the principal component analysis in the CUDA/Eigen DLL
The code to call CUDA and Eigen’s principal component analysis functions from the C# side was written as follows.
PrincipalComponentAnalysisWithCuda.dll is the name of a DLL that performs principal component analysis using CUDA and Eigen. The last parameter, calculation_method, specifies whether to execute the function using CUDA or Eigen.
The class CudaCppDllFunctions in the code below is an unsafe class so that pointers can be used from C#. In addition, a configuration change was applied to the WPF application property settings to allow code with the unsafe keyword to be compiled.
using System.Runtime.InteropServices;
using System.Security;
namespace CifarPrincipalComponentAnalysis.Utilities;
internal static unsafe class CudaCppDllFunctions
{
[DllImport("PrincipalComponentAnalysisWithCuda.dll"), SuppressUnmanagedCodeSecurity]
public static extern void solve_principal_component_analysis([In] double* m_array_input,
int rows,
int columns,
[Out] double* v_array_mean_out,
[Out] double* m_array_cov_out,
[Out] double* v_array_eigenvalues_out,
[Out] double* m_array_eigenvectors_out,
int calculation_method);
}
The C# code calling the static method solve_principal_component_analysis in the above code is as follows.
The last parameter of solve_principal_component_analysis is set to CALCULATE_WITH_CUDA or CALCULATE_WITH_EIGEN to switch whether the principal component analysis is performed with CUDA or Eigen.
Prepare a two-dimensional array X_input containing the input data, allocate memory space for a one-dimensional array and two-dimensional arrays _vectorMean, X_cov, _vectorEigenvalues, and _matrixEigenvectors containing the output data, and then CudaCppDllFunctions.solve_principal_component_analysis method is called.
To pass C# one-dimensional and two-dimensional arrays by pointer, the code use an “unsafe block” and use “fixed” in it.
double[,]? X_input = new double[numberOfImages, ImageDataSize];
for (int row = 0; row < numberOfImages; row++)
{
for (int column_i = 0; column_i < ImageAreaSize; column_i++)
{
X_input[row, 3 * column_i] = (double) _dataImages[row].BlueChannelData[column_i]; // blue
X_input[row, 3 * column_i + 1] = (double) _dataImages[row].GreenChannelData[column_i]; // green
X_input[row, 3 * column_i + 2] = (double) _dataImages[row].RedChannelData[column_i]; // red
}
}
double[,]? X_cov;
#if PCA_WITH_CUDA
//
// Use CUDA (cuBLAS and cuSOLVER) to calculate PCA
//
_vectorMean = new double[ImageDataSize];
X_cov = new double[ImageDataSize, ImageDataSize];
_vectorEigenvalues = new double[ImageDataSize];
_matrixEigenvectors = new double[ImageDataSize, ImageDataSize];
unsafe
{
fixed (double* m_array_input = X_input,
v_array_mean_out = _vectorMean,
m_array_cov_out = X_cov,
v_array_eigenvalues_out = _vectorEigenvalues,
m_array_eigenvectors_out = _matrixEigenvectors)
{
CudaCppDllFunctions.solve_principal_component_analysis(m_array_input,
numberOfImages,
ImageDataSize,
v_array_mean_out,
m_array_cov_out,
v_array_eigenvalues_out,
m_array_eigenvectors_out,
CALCULATE_WITH_CUDA);
}
}
#elif PCA_WITH_EIGEN
//
// Use Eigen to calculate PCA
//
_vectorMean = new double[ImageDataSize];
X_cov = new double[ImageDataSize, ImageDataSize];
_vectorEigenvalues = new double[ImageDataSize];
_matrixEigenvectors = new double[ImageDataSize, ImageDataSize];
unsafe
{
fixed (double* m_array_input = X_input,
v_array_mean_out = _vectorMean,
m_array_cov_out = X_cov,
v_array_eigenvalues_out = _vectorEigenvalues,
m_array_eigenvectors_out = _matrixEigenvectors)
{
CudaCppDllFunctions.solve_principal_component_analysis(m_array_input,
numberOfImages,
ImageDataSize,
v_array_mean_out,
m_array_cov_out,
v_array_eigenvalues_out,
m_array_eigenvectors_out,
CALCULATE_WITH_EIGEN);
}
}
#else
2.7. Operation Confirmation
Select Release build to build two projects, a WPF application and a CUDA C/C++ DLL.
Then, in Git Bash, go to the CifarPrincipalComponentAnalysisWithCuda/bin/Release/net8.0-windows directory and run the following command to launch CifarPrincipalComponentAnalysisWithCuda.exe by executing the following command.
$ ./CifarPrincipalComponentAnalysisWithCuda.exe
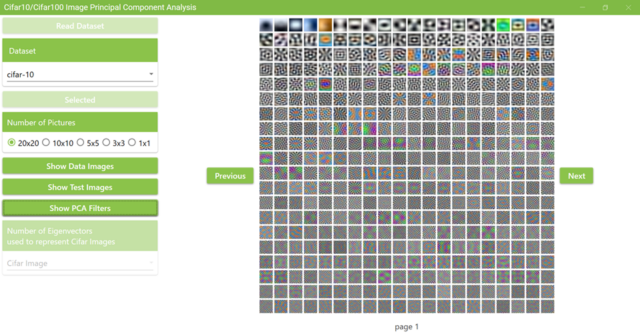
After starting the application, read the data in Cifar10 or Cifar100 following the same procedure as shown on this page. Then click the “Show PCA Filters” button and a message box will appear as shown in the image below.
Once a principal component analysis is executed, the pre-computed principal component analysis results will be used. The data resulting from the principal component analysis is stored in the directory containing the Cifar10 and Cifar100 data. Delete the data resulting from the principal component analysis and click the “Show PCA Filters” button to run the principal component analysis calculation again.
Running CifarPrincipalComponentAnalysisWithCuda.exe from Git Bash to perform a principal component analysis will output the following log to the console. The following logs are generated when __ENABLE_CONSOLE_TEST_CODES__ is enabled and the confirmation code for the calculation results of principal component analysis is executed and output to the console. The logs and images visualizing the principal component vectors when computed with CUDA and Eigen are arranged in order.
Log when calculated with CUDA (__ENABLE_CONSOLE_TEST_CODES__ is enabled)
fukagai@ESPRIMO_WD2H2 MINGW64 /c/repos/cifar10-cifar100-principal-component-analysis-with-cuda/CifarPrincipalComponentAnalysisWithCuda/bin/Release/net8.0-windows (main) $ ./CifarPrincipalComponentAnalysisWithCuda.exe PCA calculation is started. --- C++ codes (START) --- --- solve_principal_component_analysis (START) --- M_input: 63, ..., 239 M_input: ...... M_input: 123, ..., 163 V_mean: 132.554, ..., 126.639 M_input - V_mean: -69.5538, ..., 106.446 M_input - V_mean: ...... M_input - V_mean: -3.63908, ..., 36.3609 cusolverDnXsyevd_bufferSize: workspaceInBytesOnDevice = 226726024 cusolverDnXsyevd_bufferSize: workspaceInBytesOnHost = 0 after Xsyevd: info = 0 M_cov is prepared. 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 eigenvalues 1.79996e+11, ..., 5160.25 eigenvectors 0.0311112, ..., 0.0018612 ... 0.015737, ..., -0.00511573 Check Result: M_cov * V 5.5999e+09, ..., 9.60427 ... 2.83261e+09, ..., -26.3985 Check Result: V * L 5.5999e+09, ..., 9.60427 ... 2.83261e+09, ..., -26.3985 Check Result: V V^t 1, ..., -6.9931e-17 ... -6.9931e-17, ..., 1 Check Result: V L V^t 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 --- solve_principal_component_analysis (END) --- --- C++ codes (END) --- PCA calculation processing time is 00:00:29.1973187
Visualized image of the obtained principal component vectors arranged in order from the first principal component to the 400th principal component
Log when calculated with Eigen (__ENABLE_CONSOLE_TEST_CODES__ is enabled)
fukagai@ESPRIMO_WD2H2 MINGW64 /c/repos/cifar10-cifar100-principal-component-analysis-with-cuda/CifarPrincipalComponentAnalysisWithCuda/bin/Release/net8.0-windows (main) $ ./CifarPrincipalComponentAnalysisWithCuda.exe PCA calculation is started. --- C++ codes (START) --- --- solve_principal_component_analysis (START) --- M_input is prepared. 63, ..., 239 ...... 123, ..., 163 V_mean is prepared. 132.554, ..., 126.639 M_input - V_mean is prepared. -69.5538, ..., 106.446 ...... -3.63908, ..., 36.3609 M_cov is prepared. 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 eigenvalues 1.79996e+11, ..., 5160.25 eigenvectors 0.0311112, ..., -0.0018612 ... 0.015737, ..., 0.00511573 M_cov is prepared. 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 eigenvalues 1.79996e+11, ..., 5160.25 eigenvectors 0.0311112, ..., -0.0018612 ... 0.015737, ..., 0.00511573 Check Result: M_cov * V 5.5999e+09, ..., -9.60427 ... 2.83261e+09, ..., 26.3985 Check Result: V * L 5.5999e+09, ..., -9.60427 ... 2.83261e+09, ..., 26.3985 Check Result: V V^t 1, ..., -8.32017e-16 ... -8.32017e-16, ..., 1 Check Result: V L V^t 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 --- solve_principal_component_analysis (END) --- --- C++ codes (END) --- PCA calculation processing time is 00:02:10.3043911
Visualized image of the obtained principal component vectors arranged in order from the first principal component to the 400th principal component
There is a difference between the images visualizing principal component vectors computed by CUDA and Eigen. This is because the principal component vectors contain vectors whose orientations are opposite in the CUDA and Eigen calculation results.
The highlighted rows in the log above show the four corner values omitting the middle of the matrix of principal component vectors. The principal component vectors are ordered starting with the principal component vector corresponding to the largest eigenvalue, starting with the first column. The principal component vectors in column 1 have the same direction, but the principal component vectors in column 3,072 have opposite directions between CUDA and Eigen results. Because of these oppositely oriented vectors, there are differences in the images visualizing the resulting principal component vectors.
Also, because the confirmation matrix calculation is performed with __ENABLE_CONSOLE_TEST_CODES__ enabled, the calculation time output to the log is longer than when __ENABLE_CONSOLE_TEST_CODES__ is disabled.
3. Computation Time
The table summarizes the conditions and computation times for running a principal component analysis using Cifar10 training data as input on an ESPRIMO WD2/H2 desktop computer. Calculation times were checked with __ENABLE_CONSOLE_TEST_CODES__ disabled.
| Desktop PC | ESPRIMO WD2/H2 | |
| Processor | 13th Gen Intel(R) Core(TM) i5-13400 2.50 GHz | |
| GPGPU | NVIDIA GeForce GTX 1650 | |
| RAM | 16.0 GB (15.2 GB available) | |
| System type | 64-bit operating system, x64-based processor | |
| Edition | Windows 11 Pro | |
| Version | 23H2 | |
| OS Build | 22631.3374 | |
| TargetFramework | net8.0-windows | |
| Principal Component Analysis using Eigen 3.4.0 | After calculating the covariance matrix, eigenvalue decomposition is performed with SelfAdjointEigenSolver. | Calculation time: 1 minutes 54.84 seconds |
| Principal Component Analysis using CUDA Toolkit 12.4 | Run principal component analysis calculation with cuBLAS, cuSOLVER, and thrust | Calculation time: 12.01 seconds |