Principal component analysis of Cifar10/Cifar100 image dataset in C# (using C++ Eigen)
1. Overview
I created a C# program for principal component analysis of the Cifar10/Cifar100 image data set and wrote a description on this page before.
C#’s Accord.NET library was used to compute the principal component analysis, and the covariance matrix was decomposed into singular values with Accord.NET’s SingularValueDecomposition. It took about 2 hours of computation time on my Lifebook WU2/D2 laptop (model FMVWD2U27).
To speed up this calculation, the principal component analysis calculation, which was previously performed in C# using Accord.NET, is performed in C++ using Eigen. After obtaining the covariance matrix, eigenvalue decomposition is performed using SelfAdjointEigenSolver, which performs eigenvalue decomposition of a symmetric matrix. The computation time for principal component analysis was reduced to about 2 minutes and 30 seconds.
The calculation of principal component analysis in C# was also modified slightly, so that the covariance matrix is decomposed into eigenvalues using EigenvalueDecomposition in Accord.NET. Although it took more computation time than when computed using Eigen in C++, the computation time was shorter than when computed using singular value decomposition, taking about 40 minutes.
The source code has been placed in the following GitHub repository.
https://github.com/fukagai-takuya/cifar10-cifar100-principal-component-analysis-with-eigen/
2. Implementation
2.1. Download Eigen
I ran the following command in Git Bash to download Eigen to “C:\dev\eigen”.
$ cd /c/dev/ $ git clone https://gitlab.com/libeigen/eigen.git
2.2. Create DLL which uses Eigen in C++
I have added a C++ DLL project to a WPF application solution for principal component analysis of Cifar10/Cifar100 image datasets created in Visual Studio 2022 using C#.
The solution after the addition is a solution consisting of two projects: a WPF application and a C++ DLL.
The target OS for the WPF application is set to “Windows” and the target OS version to “7.0”. I also changed the target framework from “.NET 6.0” to “.NET 8.0”, although it is not necessary to do so.
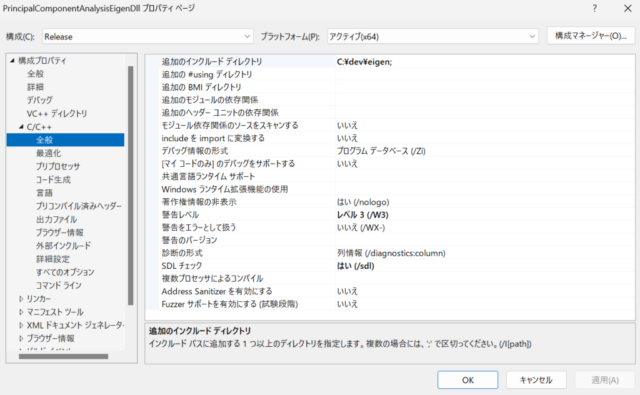
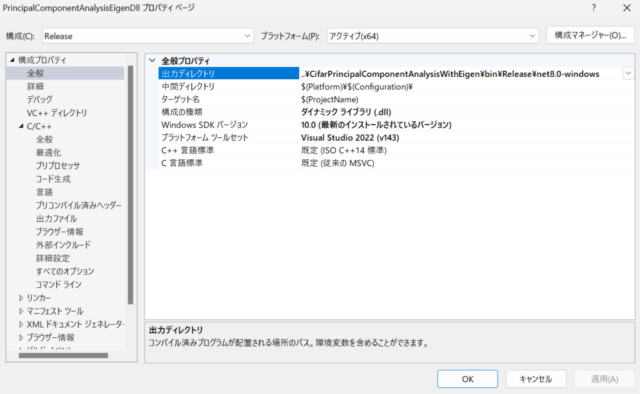
I selected the Release build from the project properties for the C++ DLL and set the “Additional include directories” to “C:\dev\eigen;” as shown in the center image below. Also, as shown in the right image below, I changed the output directory of the C++ DLL to the directory where the executable files of the Release-built WPF application are output. Since precompiled headers are not used, I selected “Do not use precompiled headers” in the project properties.
2.3. Computing Principal Component Analysis with Eigen in C++
A file PrincipalComponentAnalysisEigen.cpp with the following C++ code was added to the C++ DLL project.
The function solve_principal_component_analysis is a function called from C# code. I added extern “C” __declspec(dllexport) before the function declaration. #define DLLEXPORT is used to add it.
The function solve_principal_component_analysis takes input data as a two-dimensional array (m_array_input). The number of rows in this two-dimensional array is the number of sample data, and the number of columns is the size of the sample data vector.
The function returns the mean vector of the input sample data (v_array_mean_out), the covariance matrix (m_array_cov_out), a vector of eigenvalues of the covariance matrix in descending order (v_array_eigenvalues_out), and a matrix of eigenvectors (column vectors) of the covariance matrix in order of their corresponding eigenvalues from left to right (m_array_eigenvectors_out).
As noted in the comments of the code below, the data order of a C# two-dimensional array is Row Major, but Eigen’s Matrix is Column Major by default. The data is specified to mapped to a Row Major in the Eigen’s Matrix. The same is true for the output 2D array.
An array of eigenvalues of the solution of SelfAdjointEigenSolver that performs eigenvalue decomposition can be obtained with eigenvalues(). The obtained eigenvalues are arranged in ascending order, but here reverse() is applied to obtain the eigenvalues in descending order. Eigenvectors are similarly arranged, with the eigenvectors (column vectors) ordered from the left column, obtained with eigenvectors() and then inverted with rowwise().reverse() to match the order of the eigenvalues. This operation reverses the order of eigenvectors aligned as column vectors in the row direction.
The code below also includes code that checks the execution results and outputs the results to the console.
#define DLLEXPORT extern "C" __declspec(dllexport)
#include <iostream>
#include <Eigen/Core>
#include <Eigen/Eigenvalues>
using namespace std;
using namespace Eigen;
DLLEXPORT void solve_principal_component_analysis(double* m_array_input,
const int rows,
const int columns,
double* v_array_mean_out,
double* m_array_cov_out,
double* v_array_eigenvalues_out,
double* m_array_eigenvectors_out)
{
cout << "--- C++ codes (START) ---" << endl;
cout << "--- solve_principal_component_analysis (START) ---" << endl;
// Map m_array_input to MatrixXd
// rows: Number of sample row vectors
// columns: Size of sample row vectors
// - Make memory array Row Major to map m_array_input (Eigen's default order is Column Major)
// - C# two dimensional array double[,] is Row Major
Map<Matrix<double, Dynamic, Dynamic, RowMajor>> m_input(m_array_input, rows, columns);
cout << "m_input is prepared." << endl;
// ---------------------------------------------------------------
// Calculation of Covariance Matrix
// ---------------------------------------------------------------
// Map v_array_mean_out to VectorXd
// - The size of mean vector is columns
Map<VectorXd> v_mean(v_array_mean_out, columns);
// Calculate the mean of sample row vectors
v_mean = m_input.colwise().mean();
cout << "v_mean" << endl;
cout << v_mean(0) << ", ..., " << v_mean(columns - 1) << endl << endl;
// Subtract v_mean.transpose() from each sample row vector
m_input = m_input.rowwise() - v_mean.transpose();
// Map m_array_cov_out to MatrixXd
// - The size of rows and columns are the same as the input sample row vectors
// - Make memory array Row Major to map m_array_cov_out
Map<Matrix<double, Dynamic, Dynamic, RowMajor>> m_cov(m_array_cov_out, columns, columns);
// Calculate covariance matrix
// - Ignore the effect of constant multiplication
// - Skip division by N or N - 1 (N is sample size)
m_cov = m_input.adjoint() * m_input;
cout << "m_cov is prepared." << endl;
cout << m_cov(0, 0) << ", ..., " << m_cov(0, columns - 1) << endl;
cout << "..." << endl;
cout << m_cov(columns - 1, 0) << ", ..., " << m_cov(columns - 1, columns - 1) << endl << endl;
// ---------------------------------------------------------------
// Calculate Eigendecomposition of a covariance matrix
// ---------------------------------------------------------------
SelfAdjointEigenSolver<MatrixXd> esolver(m_cov);
// Map v_array_eigenvalues_out to VectorXd
Map<VectorXd> eigenvalues(v_array_eigenvalues_out, columns);
// Apply reverse() to make the order of eigenvalues decreasing order
eigenvalues = esolver.eigenvalues().reverse().eval();
cout << "eigenvalues" << endl;
cout << eigenvalues(0) << ", ..., " << eigenvalues(columns - 1) << endl << endl;
// Map m_array_eigenvectors_out to MatrixXd
// - Make memory array Row Major to map m_array_cov_out
Map<Matrix<double, Dynamic, Dynamic, RowMajor>> eigenvectors(m_array_eigenvectors_out, columns, columns);
// Apply reverse() to eigenvectors because the order of eigenvalues are reversed
eigenvectors = esolver.eigenvectors().rowwise().reverse().eval();
cout << "eigenvectors" << endl;
cout << eigenvectors(0, 0) << ", ..., " << eigenvectors(0, columns - 1) << endl;
cout << "..." << endl;
cout << eigenvectors(columns - 1, 0) << ", ..., " << eigenvectors(columns - 1, columns - 1) << endl << endl;
cout << "Check Result: P L P^t" << endl;
MatrixXd PLPt = eigenvectors * eigenvalues.asDiagonal() * eigenvectors.transpose();
cout << PLPt(0, 0) << ", ..., " << PLPt(0, columns - 1) << endl;
cout << "..." << endl;
cout << PLPt(columns - 1, 0) << ", ..., " << PLPt(columns - 1, columns - 1) << endl << endl;
cout << "--- solve_principal_component_analysis (END) ---" << endl;
cout << "--- C++ codes (END) ---" << endl;
}
2.4. C# code that calls the C++ Principal Component Analysis function
A file Utilities/EigenCppDllFunctions.cs with the following code is prepared in the WPF application project to call the C++ DLL function solve_principal_component_analysis. PrincipalComponentAnalysisEigenDll.dll in the code below is the name of the C++ DLL generated by the project in Section 2.2. The configuration in Section 2.2. ensures that this DLL is output in the same directory as the WPF application executable.
The class EigenCppDllFunctions in the code below is an unsafe class so that pointers can be used from C#. In addition, a configuration change was applied to the WPF application property settings to allow code with the unsafe keyword to be compiled.
using System.Runtime.InteropServices;
using System.Security;
namespace CifarPrincipalComponentAnalysis.Utilities;
internal static unsafe class EigenCppDllFunctions
{
[DllImport("PrincipalComponentAnalysisEigenDll.dll"), SuppressUnmanagedCodeSecurity]
public static extern void solve_principal_component_analysis([In] double* m_array_input,
int rows,
int columns,
[Out] double* v_array_mean_out,
[Out] double* m_array_cov_out,
[Out] double* v_array_eigenvalues_out,
[Out] double* m_array_eigenvectors_out);
}
The C# code calling the static method solve_principal_component_analysis in the above code is as follows.
Prepare a two-dimensional array X_input containing the input data, allocate memory space for a one-dimensional array and two-dimensional arrays _vectorMean, X_cov, _vectorEigenvalues, and _matrixEigenvectors containing the output data, and then EigenCppDllFunctions.solve_principal_component_analysis method is called.
To pass C# one-dimensional and two-dimensional arrays by pointer, the code use an “unsafe block” and use “fixed” in it.
double[,]? X_input = new double[numberOfImages, ImageDataSize];
for (int row = 0; row < numberOfImages; row++)
{
for (int column_i = 0; column_i < ImageAreaSize; column_i++)
{
X_input[row, 3 * column_i] = (double) _dataImages[row].BlueChannelData[column_i]; // blue
X_input[row, 3 * column_i + 1] = (double) _dataImages[row].GreenChannelData[column_i]; // green
X_input[row, 3 * column_i + 2] = (double) _dataImages[row].RedChannelData[column_i]; // red
}
}
double[,]? X_cov;
#if USE_EIGEN
//
// Use Eigen (C++ library) to calculate PCA
//
_vectorMean = new double[ImageDataSize];
X_cov = new double[ImageDataSize, ImageDataSize];
_vectorEigenvalues = new double[ImageDataSize];
_matrixEigenvectors = new double[ImageDataSize, ImageDataSize];
unsafe
{
fixed (double* m_array_input = X_input,
v_array_mean_out = _vectorMean,
m_array_cov_out = X_cov,
v_array_eigenvalues_out = _vectorEigenvalues,
m_array_eigenvectors_out = _matrixEigenvectors)
{
EigenCppDllFunctions.solve_principal_component_analysis(m_array_input,
numberOfImages,
ImageDataSize,
v_array_mean_out,
m_array_cov_out,
v_array_eigenvalues_out,
m_array_eigenvectors_out);
}
}
#else
2.5. When build without C++ DLL
In the file Models/CifarDataset.cs, USE_EIGEN is defined as shown in the code below. This condition will generate a program that uses Eigen in C++.
#define USE_EIGEN
Commenting out as follows will generate a program that uses EigenvalueDecomposition in Accord.NET.
//#define USE_EIGEN
2.6. Operation Confirmation
Select Release build to build two projects, a WPF application and a C++ DLL.
Then, in Git Bash, go to the CifarPrincipalComponentAnalysisWithEigen/bin/Release/net8.0-windows directory and run the following command to launch CifarPrincipalComponentAnalysisWithEigen.exe by executing the following command.
$ ./CifarPrincipalComponentAnalysisWithEigen.exe
After starting the application, read the data in Cifar10 or Cifar100 following the same procedure as shown on this page. Then click the “Show PCA Filters” button and a message box will appear as shown in the image below.
Once a principal component analysis is executed, the pre-computed principal component analysis results will be used. The data resulting from the principal component analysis is stored in the directory containing the Cifar10 and Cifar100 data. Delete the data resulting from the principal component analysis and click the “Show PCA Filters” button to run the principal component analysis calculation again.
Running CifarPrincipalComponentAnalysisWithEigen.exe from Git Bash to run a principal component analysis will produce the following log in the console. The log also includes a measurement of the run time of the principal component analysis.
$ ./CifarPrincipalComponentAnalysisWithEigen.exe PCA calculation is started. --- C++ codes (START) --- --- solve_principal_component_analysis (START) --- m_input is prepared. v_mean 132.554, ..., 126.639 m_cov is prepared. 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 eigenvalues 1.79996e+11, ..., 5160.25 eigenvectors 0.0311112, ..., -0.0018612 ... 0.015737, ..., 0.00511573 Check Result: P L P^t 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 --- solve_principal_component_analysis (END) --- --- C++ codes (END) --- PCA calculation processing time is 00:01:53.9159126 _vectorMean: 132.5538, ..., 126.63908 X_cov: 323601651.2779998, ..., 66694125.874800056 ... X_cov: 66694125.874800056, ..., 210766896.83767992 _vectorEigenvalues: 179996402559.84167, ..., 5160.249723685157 _matrixEigenvectors: 0.03111119420487357, ..., -0.001861201694741981 ... _matrixEigenvectors: 0.015737041116741294, ..., 0.005115732425291488 P^T P: 1.0000000000000042, ..., -1.5368565794982025E-17 ... P^T P: -1.5368565794982025E-17, ..., 1.000000000000006 PLP^T: 323601651.27801186, ..., 66694125.87479978 ... PLP^T: 66694125.87479978, ..., 210766896.83769244
3. Computation Time
The table below shows the conditions and computation time when I performed a principal component analysis using Cifar10 training data as input on my Lifebook WU2/D2 (model FMVWD2U27) laptop and ESPRIMO WD2/H2 desktop computer.
| Laptop | Lifebook WU2/D2 (model FMVWD2U27) | |
| Processor | Intel(R) Core(TM) i3-8145U CPU @ 2.10GHz 2.30 GHz | |
| RAM | 8.00 GB (7.75 GB available) | |
| System type | 64-bit operating system, x64-based processor | |
| Edition | Windows 11 Home | |
| Version | 22H2 | |
| OS Build | 22621.3155 | |
| TargetFramework | net8.0-windows | |
| Principal Component Analysis using Accord.Math 3.8.0 | After calculating the covariance matrix, eigenvalue decomposition is performed with EigenvalueDecomposition. | Calculation time: 39 minutes 19 seconds |
| Principal Component Analysis using Eigen 3.4.0 | After calculating the covariance matrix, eigenvalue decomposition is performed with SelfAdjointEigenSolver. | Calculation time: 2 minutes 34 seconds |
| Desktop PC | ESPRIMO WD2/H2 | |
| Processor | 13th Gen Intel(R) Core(TM) i5-13400 2.50 GHz | |
| RAM | 16.0 GB (15.2 GB available) | |
| System type | 64-bit operating system, x64-based processor | |
| Edition | Windows 11 Pro | |
| Version | 23H2 | |
| OS Build | 22631.3155 | |
| TargetFramework | net8.0-windows | |
| Principal Component Analysis using Accord.Math 3.8.0 | After calculating the covariance matrix, eigenvalue decomposition is performed with EigenvalueDecomposition. | Calculation time: 23 minutes 32 seconds |
| Principal Component Analysis using Eigen 3.4.0 | After calculating the covariance matrix, eigenvalue decomposition is performed with SelfAdjointEigenSolver. | Calculation time: 1 minutes 54 seconds |