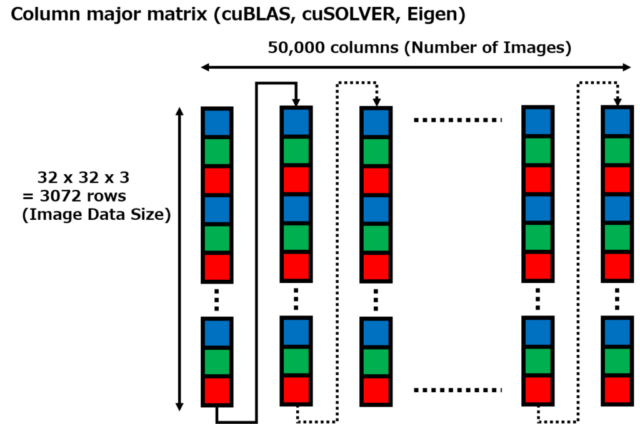Cifar10/Cifar100の画像データセットをC#で主成分分析 (CUDAを利用)
1. 概要
以前、Cifar10/Cifar100の画像データセットを主成分分析するC#のプログラムを作成し、こちらの説明ページを用意しました。
上記のプログラムでは、50,000枚の画像データ(3,072のRGB値)の主成分分析に2時間ほどの時間を要していました。プログラムはノートパソコンLifebook WU2/D2(型名 FMVWD2U27)で実行しました。この主成分分析をC++のEigenで計算するようにしたところ、計算時間は約2分30秒に短縮されました。デスクトップパソコンESPRIMO WD2/H2でも計算時間を確認したところ、C++のEigenを使用した主成分分析の計算時間は約2分でした。これについてはこちらに説明ページを用意しました。
今回は、主成分分析の計算をCUDAに書き換え、GPGPUで実行しました。デスクトップパソコンESPRIMO WD2/H2でNVIDIA GeForce GTX 1650を使って計算し、計算時間が約12秒に短縮されたのを確認しました。
CUDA版のソースコードは下記のGitHubリポジトリに置きました。
https://github.com/fukagai-takuya/cifar10-cifar100-principal-component-analysis-with-cuda
2. 実装方法
2.1. CUDA Toolkit 12.4のインストール
下記のページからCUDA Toolkit 12.4のWindows版をダウンロードし、Windows 11のデスクトップパソコンESPRIMO WD2/H2にインストールしました。
https://developer.nvidia.com/cuda-downloads
2.2. CUDAを使用するDLLの準備
Cifar10/Cifar100の画像データセットをC#で表示し、C++のEigenを使用したDLLで主成分分析するWPFアプリケーションのこちらのVisual Studio 2022のソリューションのDLL部分をCUDA実装に書き換えました。計算時間の比較のため、C++のEigenを使用した主成分分析の計算も残すようにしました。
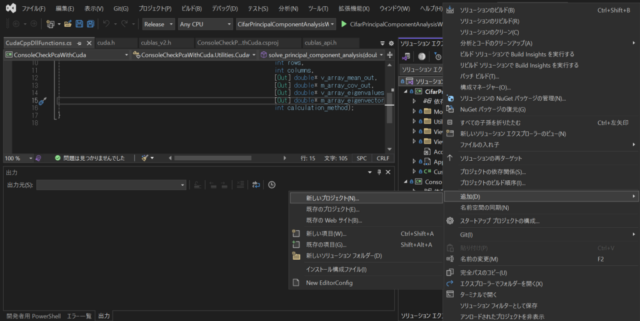
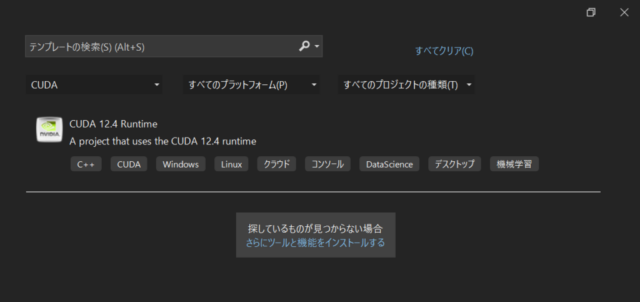
Releaseビルドを対象とし、C++のEigenを使用したプロジェクトを削除した後、左下の画像のようにソリューションに新しいプロジェクトを追加しました。追加するプロジェクトには、中央下の画像のようにCUDA 12.4 Runtimeを選択しました。
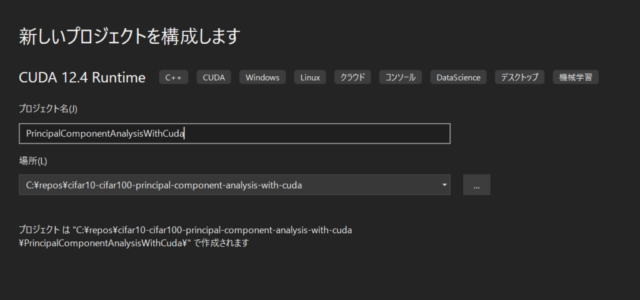
プロジェクト名は右下の画像のようにPrincipalComponentAnalysisWithCudaにしました。
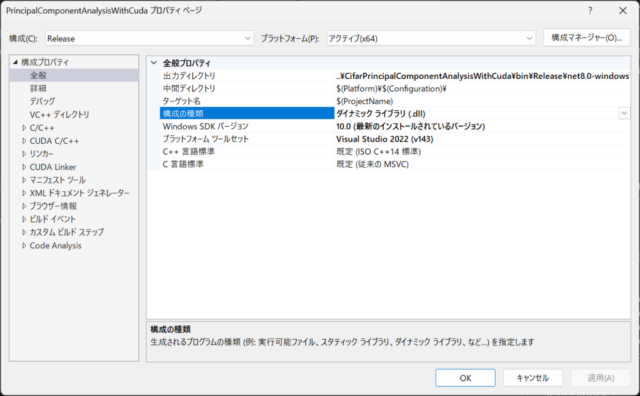
追加したCUDA 12.4 Runtimeはコンソールアプリケーションなため、左下の画像のようにプロパティの構成の種類をダイナミックライブラリ(.dll)に変更しました。また、DLLの出力ディレクトリをC#プロジェクトの実行ファイル(.exe)が出力されるディレクトリに変更しました。
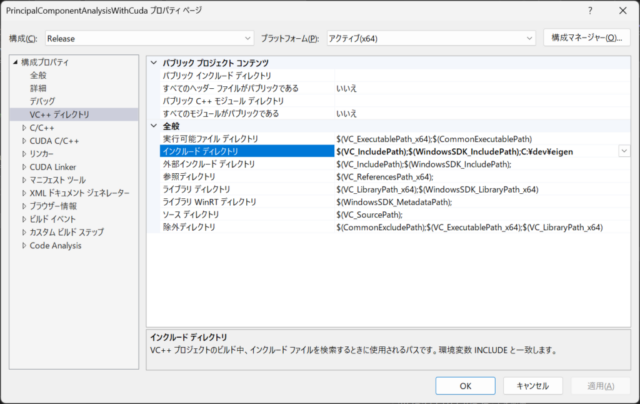
C++のEigenを使用した主成分分析の関数もDLLに含めることにしたため、中央下の画像のようにEigenをインストールしたディレクトリC:\dev\eigenをインクルードディレクトリに追加しました。
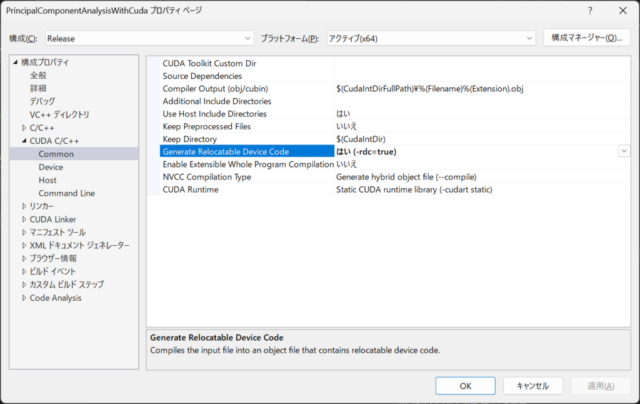
拡張子.cuのCUDAを使用するコードと拡張子.cppのEigenを使用するコードに分割してDLLを作成することにしたため、右下の画像のようにCUDA C/C++の設定で-rdc=trueを選択しています。(拡張子.cuのファイルを複数のファイルからなるDLLの一部としてビルドする場合、-rdc=trueを選択します。)
Eigenを使用したコードを拡張子.cuのファイル内に記述したところ、Eigenを使用した主成分分析の処理時間が長くなったため、上記のように分割しました。ファイルを分割して一つのDLLを作成したところ、Eigenを使用した主成分分析の処理時間はこちらにページに記載した処理時間と同程度になりました。
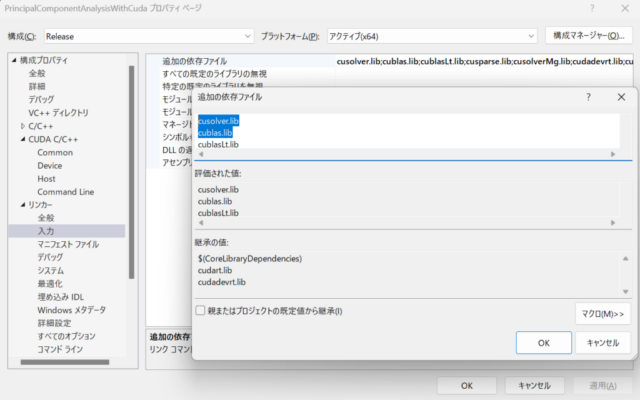
cuBLASとcuSOLVERライブラリを使用するため、下の一番目の画像のようにリンカーの入力の追加の依存ファイルにcusolver.libとcublas.libを追加しました。
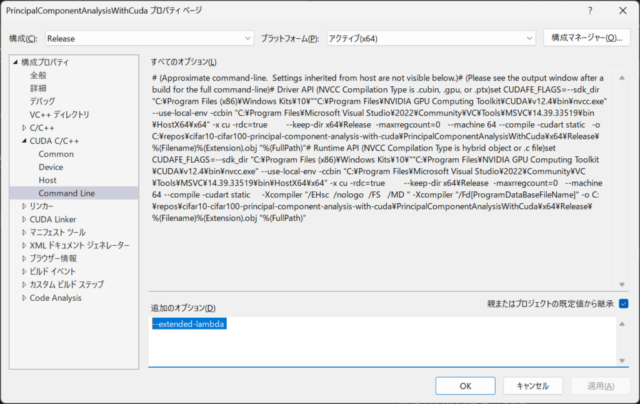
ラムダ式を利用するコードを使用するため、下の二番目の画像のようにCUDA C/C++のコマンドラインオプションとして–extended-lambdaを追加しました。
下の三番目の画像のようにCUDA C/C++のホスト側のRuntime LibraryとしてMulti-Threaded DLL (/MD)を選択するようにしました。
下の四番目の画像のようにCUDA C/C++のDeviceのCode Generationとして、使用したGPGPU NVIDIA GeForce GTX 1650に対応するcompute_75,sm_75;を指定しました。
こちらのソリューションにはC#のConsoleCheckPcaWithCudaというプロジェクトも含まれています。CUDA実装したDLLによる計算の簡単な確認のために用意したコンソールプログラムのプロジェクトです。
2.3. C++のDLLによる主成分分析の計算 (CUDAとEigenを使用した計算の共通部分)
CUDAとEigenで主成分分析を実行するDLLのプロジェクトには下記の4つのファイルを追加しました。
- PrincipalComponentAnalysis.h
- PrincipalComponentAnalysis.cpp
- PrincipalComponentAnalysisWithCuda.cu
- PrincipalComponentAnalysisWithEigen.cpp
PrincipalComponentAnalysis.h は下記のようなヘッダーファイルです。
C#のプログラムから主成分分析の計算をCUDAかEigenのどちらで実行するかをパラメータで受け取り、パラメータに応じてヘッダーファイルに記載した二つの関数のいずれかを実行するようにしています。
主成分分析の計算の途中経過と計算結果をコンソールに出力するか否かを __ENABLE_CONSOLE_TEST_CODES__ で切り替えるようにしています。固有値分解の結果を確認する計算も含まれており、__ENABLE_CONSOLE_TEST_CODES__ を有効にするか否かで実行時間に差が出ます。計算時間を評価する際には下記のコードのように __ENABLE_CONSOLE_TEST_CODES__ を無効にしました。
#pragma once
#define DLLEXPORT extern "C" __declspec(dllexport)
//#define __ENABLE_CONSOLE_TEST_CODES__
#include <iostream>
#include <vector>
#include <cuda_runtime.h>
#include <cublas_v2.h>
#include <cusolverDn.h>
#include <library_types.h>
#include <thrust/device_vector.h>
#include <thrust/reverse.h>
#include <thrust/for_each.h>
#include <Eigen/Core>
#include <Eigen/Eigenvalues>
/**
* Calculate Principal Component Analysis with Eigen (C++ implementation)
*
* - Since Eigen matrix is column-major, m_array_input's rows and columns are swapped from C# interface
*
* @param m_array_input Pointer to an input matrix values (length: rows * columns): column-major matrix (M_input)
* @param columns Number of columns of an input matrix: Number of sample vectors
* @param rows Number of rows of an input matrix: Size of sample vector
* @param v_array_mean_out Pointer to an output mean vector (length: rows): Mean of sample vectors
* @param m_array_cov_out Pointer to an output covariance martix (length: rows * rows): Covariance matrix of sample vectors
* @param v_array_eigenvalues_out Pointer to an output eigenvalues vector (length: rows): Eigenvalues of covariance matrix
* @param m_array_eigenvectors_out Pointer to an output eigenvectors martix (length: rows * rows): Eigenvectors of covariance matrix (row-major)
*/
void solve_principal_component_analysis_with_eigen(double* m_array_input,
const int columns,
const int rows,
double* v_array_mean_out,
double* m_array_cov_out,
double* v_array_eigenvalues_out,
double* m_array_eigenvectors_out);
/**
* Calculate Principal Component Analysis with cuBLAS and cuSOLVER (CUDA implementation)
*
* - Since cuBLAS and cuSOLVER matrix is column-major, m_array_input's rows and columns are swapped from C# interface
*
* @param m_array_input Pointer to an input matrix values (length: rows * columns): column-major matrix (M_input)
* @param columns Number of columns of an input matrix: Number of sample vectors
* @param rows Number of rows of an input matrix: Size of sample vector
* @param v_array_mean_out Pointer to an output mean vector (length: rows): Mean of sample vectors
* @param m_array_cov_out Pointer to an output covariance martix (length: rows * rows): Covariance matrix of sample vectors
* @param v_array_eigenvalues_out Pointer to an output eigenvalues vector (length: rows): Eigenvalues of covariance matrix
* @param m_array_eigenvectors_out Pointer to an output eigenvectors martix (length: rows * rows): Eigenvectors of covariance matrix (row-major)
*/
void solve_principal_component_analysis_with_cuda(const double* m_array_input,
const int columns,
const int rows,
double* v_array_mean_out,
double* m_array_cov_out,
double* v_array_eigenvalues_out,
double* m_array_eigenvectors_out);
PrincipalComponentAnalysis.cppは下記のようなファイルです。C#のコードからは下記のファイルの関数 solve_principal_component_analysisを呼びます。関数の最後の引数calculation_methodでCUDAを使用した主成分分析を実行するかC++のEigenを使用した主成分分析を実行するかを指定します。
C#から呼ぶことができるようにするため、ヘッダーファイルに記載したDLLEXPORTを関数定義の前に付けDLLEXPORT void solve_principal_component_analysisのように記載しています。
#ifdef __ENABLE_CONSOLE_TEST_CODES__ から #endif 内に記載したのは主成分分析の計算結果を確認するコードで、計算された共分散行列、降順に並べられた共分散行列の固有値と固有ベクトル、共分散行列の固有値分解の確認結果をコンソールに出力しています。コンソール出力のM_covは共分散行列、Vは固有ベクトルを1列目から順に並べた行列、VtはVの転置行列、Lは固有値を対角成分として並べた対角行列です。固有ベクトルを並べた行列Vには、降順に並べられた固有値に対応する固有ベクトルを1列目から順に並べています。
#include "PrincipalComponentAnalysis.h"
using namespace std;
using namespace Eigen;
/**
* Specify calculation method
* - Use Eigen for the Calculation of Principal Component Analysis
*/
const int CALCULATE_WITH_EIGEN = 0;
/**
* Specify calculation method
* - Use CUDA for the Calculation of Principal Component Analysis
*/
const int CALCULATE_WITH_CUDA = 1;
/**
* Calculate Principal Component Analysis
*
* - Since Eigen, cuBLAS and cuSOLVER matrix is column-major, m_array_input's rows and columns are swapped from C# interface
*
* @param m_array_input Pointer to an input matrix values (length: rows * columns): column-major matrix
* @param columns Number of columns of an input matrix: Number of sample vectors
* @param rows Number of rows of an input matrix: Size of sample vector
* @param v_array_mean_out Pointer to an output mean vector (length: rows): Mean of sample vectors
* @param m_array_cov_out Pointer to an output covariance martix (length: rows * rows): Covariance matrix of sample vectors
* @param v_array_eigenvalues_out Pointer to an output eigenvalues vector (length: rows): Eigenvalues of covariance matrix
* @param m_array_eigenvectors_out Pointer to an output eigenvectors martix (length: rows * rows): Eigenvectors of covariance matrix (row-major)
* @param calculation_method 0:Eigen, 1:CUDA
*/
DLLEXPORT void solve_principal_component_analysis(double* m_array_input,
const int columns,
const int rows,
double* v_array_mean_out,
double* m_array_cov_out,
double* v_array_eigenvalues_out,
double* m_array_eigenvectors_out,
const int calculation_method = CALCULATE_WITH_EIGEN)
{
cout << "--- C++ codes (START) ---" << endl;
cout << "--- solve_principal_component_analysis (START) ---" << endl;
if (calculation_method == CALCULATE_WITH_EIGEN) {
solve_principal_component_analysis_with_eigen(m_array_input,
columns,
rows,
v_array_mean_out,
m_array_cov_out,
v_array_eigenvalues_out,
m_array_eigenvectors_out);
} else if (calculation_method == CALCULATE_WITH_CUDA) {
solve_principal_component_analysis_with_cuda(m_array_input,
columns,
rows,
v_array_mean_out,
m_array_cov_out,
v_array_eigenvalues_out,
m_array_eigenvectors_out);
}
// ---------------------------------------------------------------
// Test codes (Start)
// ---------------------------------------------------------------
#ifdef __ENABLE_CONSOLE_TEST_CODES__
// Map m_array_cov_out to MatrixXd
// - The size of rows are the same as the input rows
// - Since m_array_cov_out stores values of a symmetric matrix,
// it is not affected by the difference between column-major and row-major.
Map<MatrixXd> M_cov(m_array_cov_out, rows, rows);
cout << "M_cov is prepared." << endl;
cout << M_cov(0, 0) << ", ..., " << M_cov(0, rows - 1) << endl;
cout << "..." << endl;
cout << M_cov(rows - 1, 0) << ", ..., " << M_cov(rows - 1, rows - 1) << endl << endl;
// Map v_array_eigenvalues_out to VectorXd
Map<VectorXd> eigenvalues(v_array_eigenvalues_out, rows);
cout << "eigenvalues" << endl;
cout << eigenvalues(0) << ", ..., " << eigenvalues(rows - 1) << endl << endl;
// Map m_array_eigenvectors_out to MatrixXd
// - Since m_array_eigenvectors_out is row-major map to row-major matrix
Map<Matrix<double, Dynamic, Dynamic, RowMajor>> eigenvectors(m_array_eigenvectors_out, rows, rows);
cout << "eigenvectors" << endl;
cout << eigenvectors(0, 0) << ", ..., " << eigenvectors(0, rows - 1) << endl;
cout << "..." << endl;
cout << eigenvectors(rows - 1, 0) << ", ..., " << eigenvectors(rows - 1, rows - 1) << endl << endl;
MatrixXd M_cov_V = M_cov * eigenvectors;
cout << "Check Result: M_cov * V" << endl;
cout << M_cov_V(0, 0) << ", ..., " << M_cov_V(0, rows - 1) << endl;
cout << "..." << endl;
cout << M_cov_V(rows - 1, 0) << ", ..., " << M_cov_V(rows - 1, rows - 1) << endl << endl;
MatrixXd V_L = eigenvectors * eigenvalues.asDiagonal();
cout << "Check Result: V * L" << endl;
cout << V_L(0, 0) << ", ..., " << V_L(0, rows - 1) << endl;
cout << "..." << endl;
cout << V_L(rows - 1, 0) << ", ..., " << V_L(rows - 1, rows - 1) << endl << endl;
MatrixXd VVt = eigenvectors * eigenvectors.transpose();
cout << "Check Result: V V^t" << endl;
cout << VVt(0, 0) << ", ..., " << VVt(0, rows - 1) << endl;
cout << "..." << endl;
cout << VVt(rows - 1, 0) << ", ..., " << VVt(rows - 1, rows - 1) << endl << endl;
MatrixXd VLVt = eigenvectors * eigenvalues.asDiagonal() * eigenvectors.transpose();
cout << "Check Result: V L V^t" << endl;
cout << VLVt(0, 0) << ", ..., " << VLVt(0, rows - 1) << endl;
cout << "..." << endl;
cout << VLVt(rows - 1, 0) << ", ..., " << VLVt(rows - 1, rows - 1) << endl << endl;
// ---------------------------------------------------------------
// Test codes (End)
// ---------------------------------------------------------------
#endif
cout << "--- solve_principal_component_analysis (END) ---" << endl;
cout << "--- C++ codes (END) ---" << endl;
}
2.4. CUDAによる主成分分析の計算
PrincipalComponentAnalysisWithCuda.cuでは下記のコードのようにcuBLAS、cuSOLVER、thrustを使用して主成分分析の計算を実行しています。
3,072行50,000列の行列とその転置行列の積を取り、3,072行3,072列の共分散行列を得る計算をcublasDgemmで行いました。Eigenを使用して計算した場合に比べ、計算時間を大幅に短縮することができました。
共分散行列の固有値分解は対称行列の固有値分解を実行するcuSOLVERのcusolverDnXsyevdで計算しました。
C#側で入力データを配列m_array_inputにセットした際、double型の二次元配列double[,]の各行に3,072要素からなる画像データを50,000行分セットしました。各行が1枚の画像のデータに対応しており、50,000枚の画像データをセットしました。C#の二次元配列double[,]はrow majorの順にデータを配置しているため、一次元配列m_array_inputには1行目の3,072要素、2行目の3,072要素、…、50,000行目の3,072要素の順にデータがセットされています。
cuBLASとcuSOLVERでは、行列データはcolumn majorの順に配置されているとしているため、一次元配列m_array_inputには3,072行50,000列のデータが格納されているとみなして計算しています。C#側でsolve_principal_component_analysisを呼び出した関数の第二引数rows(行数)と第三引数columns(列数)をsolve_principal_component_analysis_with_cudaでは入れ替え、第二引数をcolumns、第三引数をrowsとしています。
cusolverDnXsyevdを使用して得られた固有値は昇順に並べられており、対応する固有ベクトルを並べた行列もその順に配置されています。固有値を降順に並べ替え、固有ベクトルを並べた行列もそれに合わせて配置を変更しています。固有ベクトルの列の順を並べ替える計算にはthrust::for_eachを使用していますが、この計算でラムダ式を使用しています。そのため、上記のようにCUDA C/C++のDLLをビルドする際のコマンドラインオプションに–extended-lambdaを追加しています。
C#のコードは計算結果をrow majorで受け取ることを想定しているため、固有ベクトルを並べた行列の転置を取ってから、m_array_eigenvectors_out配列に値をコピーするようにしています。
#include "PrincipalComponentAnalysis.h"
// CUDA API error checking
#define CUDA_CHECK(err) \
do { \
cudaError_t err_ = (err); \
if (err_ != cudaSuccess) { \
std::printf("CUDA error %d at %s:%d\n", err_, __FILE__, __LINE__); \
throw std::runtime_error("CUDA error"); \
} \
} while (0)
// cublas API error checking
#define CUBLAS_CHECK(err) \
do { \
cublasStatus_t err_ = (err); \
if (err_ != CUBLAS_STATUS_SUCCESS) { \
std::printf("cublas error %d at %s:%d\n", err_, __FILE__, __LINE__); \
throw std::runtime_error("cublas error"); \
} \
} while (0)
// cusolver API error checking
#define CUSOLVER_CHECK(err) \
do { \
cusolverStatus_t err_ = (err); \
if (err_ != CUSOLVER_STATUS_SUCCESS) { \
std::printf("cusolver error %d at %s:%d\n", err_, __FILE__, __LINE__); \
throw std::runtime_error("cusolver error"); \
} \
} while (0)
template <typename T>
struct linear_index_to_row_index : public thrust::unary_function<T,T> {
T rows; // --- Number of rows
__host__ __device__ linear_index_to_row_index(T rows) : rows(rows) {}
__host__ __device__ T operator()(T i) { return i % rows; }
};
/**
* Calculate Principal Component Analysis with cuBLAS and cuSOLVER (CUDA implementation)
*
* - Since cuBLAS and cuSOLVER matrix is column-major, m_array_input's rows and columns are swapped from C# interface
*
* @param m_array_input Pointer to an input matrix values (length: rows * columns): column-major matrix (M_input)
* @param columns Number of columns of an input matrix: Number of sample vectors
* @param rows Number of rows of an input matrix: Size of sample vector
* @param v_array_mean_out Pointer to an output mean vector (length: rows): Mean of sample vectors
* @param m_array_cov_out Pointer to an output covariance martix (length: rows * rows): Covariance matrix of sample vectors
* @param v_array_eigenvalues_out Pointer to an output eigenvalues vector (length: rows): Eigenvalues of covariance matrix
* @param m_array_eigenvectors_out Pointer to an output eigenvectors martix (length: rows * rows): Eigenvectors of covariance matrix (row-major)
*/
void solve_principal_component_analysis_with_cuda(const double* m_array_input,
const int columns,
const int rows,
double* v_array_mean_out,
double* m_array_cov_out,
double* v_array_eigenvalues_out,
double* m_array_eigenvectors_out)
{
cublasHandle_t cublasH = NULL;
cudaStream_t stream = NULL;
// Create cublas handle, bind a stream
CUBLAS_CHECK(cublasCreate(&cublasH));
CUDA_CHECK(cudaStreamCreateWithFlags(&stream, cudaStreamNonBlocking));
CUBLAS_CHECK(cublasSetStream(cublasH, stream));
thrust::device_vector<double> d_M_input(rows * columns); // M_input
thrust::device_vector<double> d_V_ones(columns, 1.f); // V_ones = [1, ..., 1]^t
thrust::device_vector<double> d_V_mean(rows); // V_mean = 1 / columns * M_input * [1, ..., 1]^t
thrust::device_vector<double> d_M_cov(rows * rows); // M_cov = A * A^t (A = M_input - [V_mean, ..., V_mean])
thrust::device_vector<double> d_M_eingenvectors_row_major(rows * rows); // Eigenvectors of M_cov (row-major matrix)
CUDA_CHECK(cudaMemcpyAsync(thrust::raw_pointer_cast(d_M_input.data()), m_array_input, sizeof(double) * rows * columns,
cudaMemcpyHostToDevice, stream));
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "M_input: " << d_M_input[0] << ", ..., " << d_M_input[(columns - 1) * rows] << std::endl;
std::cout << "M_input: " << "......" << std::endl;
std::cout << "M_input: " << d_M_input[rows - 1] << ", ..., " << d_M_input[rows * columns - 1] << std::endl << std::endl;
#endif
// -------------------------------------------------------------------------------------------
// Calculation of Mean Vector: V_mean = 1 / columns * M_input * [1, ..., 1]^t
// -------------------------------------------------------------------------------------------
double alpha = 1.0 / columns;
double beta = 0.0;
CUBLAS_CHECK(cublasDgemv(cublasH, CUBLAS_OP_N, rows, columns, &alpha, thrust::raw_pointer_cast(d_M_input.data()), rows,
thrust::raw_pointer_cast(d_V_ones.data()), 1, &beta, thrust::raw_pointer_cast(d_V_mean.data()), 1));
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "V_mean: " << d_V_mean[0] << ", ..., " << d_V_mean[rows - 1] << std::endl << std::endl;
#endif
// -------------------------------------------------------------------------------------------
// Subtract mean colum vector from input Matrix columns: A = M_input - [V_mean, ..., V_mean]
// -------------------------------------------------------------------------------------------
thrust::transform(d_M_input.begin(), d_M_input.end(),
thrust::make_permutation_iterator(d_V_mean.begin(),
thrust::make_transform_iterator(thrust::make_counting_iterator(0),
linear_index_to_row_index<int>(rows))),
d_M_input.begin(),
thrust::minus<double>());
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "M_input - V_mean: " << d_M_input[0] << ", ..., " << d_M_input[(columns - 1) * rows] << std::endl;
std::cout << "M_input - V_mean: " << "......" << std::endl;
std::cout << "M_input - V_mean: " << d_M_input[rows - 1] << ", ..., " << d_M_input[rows * columns - 1] << std::endl << std::endl;
#endif
// -------------------------------------------------------------------------------------------
// Calculation of Covariance Matrix: M_cov = A * A^t (A = M_input - [V_mean, ..., V_mean])
// -------------------------------------------------------------------------------------------
alpha = 1.0;
beta = 0.0;
CUBLAS_CHECK(cublasDgemm(cublasH, CUBLAS_OP_N, CUBLAS_OP_T, rows, rows, columns, &alpha,
thrust::raw_pointer_cast(d_M_input.data()), rows,
thrust::raw_pointer_cast(d_M_input.data()), rows, &beta,
thrust::raw_pointer_cast(d_M_cov.data()), rows));
// Copy data to host
CUDA_CHECK(cudaMemcpyAsync(v_array_mean_out, thrust::raw_pointer_cast(d_V_mean.data()), sizeof(double) * rows,
cudaMemcpyDeviceToHost, stream));
CUDA_CHECK(cudaMemcpyAsync(m_array_cov_out, thrust::raw_pointer_cast(d_M_cov.data()), sizeof(double) * rows * rows,
cudaMemcpyDeviceToHost, stream));
CUDA_CHECK(cudaStreamSynchronize(stream));
// ---------------------------------------------------------------
// Eigendecomposition of a covariance matrix
// ---------------------------------------------------------------
cusolverDnHandle_t cusolverH = NULL;
cusolverDnParams_t params = NULL;
thrust::device_vector<double> d_V_eigenvalues(rows);
thrust::device_vector<int> d_info(1);
int info = 0;
size_t workspaceInBytesOnDevice = 0; // size of workspace
void *d_work = nullptr; // device workspace
size_t workspaceInBytesOnHost = 0; // size of workspace
void *h_work = nullptr; // host workspace
// Create cusolver handle, bind a stream
CUSOLVER_CHECK(cusolverDnCreate(&cusolverH));
CUSOLVER_CHECK(cusolverDnSetStream(cusolverH, stream));
CUSOLVER_CHECK(cusolverDnCreateParams(¶ms));
// Query working space of syevd
cusolverEigMode_t jobz = CUSOLVER_EIG_MODE_VECTOR; // Compute eigenvalues and eigenvectors
cublasFillMode_t uplo = CUBLAS_FILL_MODE_LOWER; // Lower triangle of d_M_cov is stored
CUSOLVER_CHECK(cusolverDnXsyevd_bufferSize(cusolverH, params, jobz, uplo, rows, CUDA_R_64F, thrust::raw_pointer_cast(d_M_cov.data()), rows,
CUDA_R_64F, thrust::raw_pointer_cast(d_V_eigenvalues.data()), CUDA_R_64F,
&workspaceInBytesOnDevice, &workspaceInBytesOnHost));
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::printf("cusolverDnXsyevd_bufferSize: workspaceInBytesOnDevice = %zu\n", workspaceInBytesOnDevice);
std::printf("cusolverDnXsyevd_bufferSize: workspaceInBytesOnHost = %zu\n", workspaceInBytesOnHost);
#endif
CUDA_CHECK(cudaMalloc(reinterpret_cast<void **>(&d_work), workspaceInBytesOnDevice));
if (workspaceInBytesOnHost > 0) {
h_work = reinterpret_cast<void *>(malloc(workspaceInBytesOnHost));
if (h_work == nullptr) {
throw std::runtime_error("Error: h_work not allocated.");
}
}
// Compute eigendecomposition
CUSOLVER_CHECK(cusolverDnXsyevd(cusolverH, params, jobz, uplo, rows, CUDA_R_64F,
thrust::raw_pointer_cast(d_M_cov.data()), rows, CUDA_R_64F,
thrust::raw_pointer_cast(d_V_eigenvalues.data()), CUDA_R_64F, d_work, workspaceInBytesOnDevice,
h_work, workspaceInBytesOnHost, thrust::raw_pointer_cast(d_info.data())));
// Apply thrust::reverse() to make the order of eigenvalues decreasing order
thrust::reverse(d_V_eigenvalues.begin(), d_V_eigenvalues.end());
// Since the order of eigenvalues is reversed,
// reverse the column order of eigenvectors matrix (column-major matrix)
int m_eigenvectors_size = rows * rows;
int m_eigenvectors_rows = rows;
int m_eigenvectors_columns = rows;
double *d_M_eigenvectors_ptr = (double *)thrust::raw_pointer_cast(d_M_cov.data());
auto counting = thrust::make_counting_iterator<int>(0);
thrust::for_each(thrust::cuda::par.on(stream), counting,
counting + (m_eigenvectors_size / 2), [=] __device__(int idx) {
int dest_row = idx % m_eigenvectors_rows;
int dest_col = idx / m_eigenvectors_rows;
int src_row = dest_row;
int src_col = (m_eigenvectors_columns - dest_col) - 1;
int src_idx = src_col * m_eigenvectors_rows + src_row;
double temp = d_M_eigenvectors_ptr[idx];
d_M_eigenvectors_ptr[idx] = d_M_eigenvectors_ptr[src_idx];
d_M_eigenvectors_ptr[src_idx] = temp;
});
// Make the order of eigenvectors matrix (column-major matrix) row-major matrix : Transpose
alpha = 1.0;
beta = 0.0;
CUBLAS_CHECK(cublasDgeam(cublasH, CUBLAS_OP_T, CUBLAS_OP_N, rows, rows, &alpha,
d_M_eigenvectors_ptr, rows, &beta,
d_M_eigenvectors_ptr, rows,
thrust::raw_pointer_cast(d_M_eingenvectors_row_major.data()), rows));
CUDA_CHECK(cudaMemcpyAsync(m_array_eigenvectors_out, thrust::raw_pointer_cast(d_M_eingenvectors_row_major.data()),
sizeof(double) * rows * rows,
cudaMemcpyDeviceToHost, stream));
CUDA_CHECK(cudaMemcpyAsync(v_array_eigenvalues_out, thrust::raw_pointer_cast(d_V_eigenvalues.data()), sizeof(double) * rows,
cudaMemcpyDeviceToHost, stream));
CUDA_CHECK(cudaMemcpyAsync(&info, thrust::raw_pointer_cast(d_info.data()), sizeof(int), cudaMemcpyDeviceToHost, stream));
CUDA_CHECK(cudaStreamSynchronize(stream));
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::printf("after Xsyevd: info = %d\n", info);
#endif
if (0 > info) {
std::printf("%d-th parameter is wrong \n", -info);
exit(1);
}
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::printf("\n\n");
#endif
// free resources
CUDA_CHECK(cudaFree(d_work));
free(h_work);
CUBLAS_CHECK(cublasDestroy(cublasH));
CUSOLVER_CHECK(cusolverDnDestroy(cusolverH));
CUDA_CHECK(cudaStreamDestroy(stream));
}
2.5. Eigenによる主成分分析の計算
PrincipalComponentAnalysisWithEigen.cppでは下記のコードのようにEigenを使用して主成分分析の計算を実行しています。
こちらのページのEigenを用いた主成分分析のコードとほぼ同じです。
Eigenの行列はデフォルトでcolumn majorなため、CUDAのコードと同様、C#側のrow majorな50,000行3,072列の二次元配列double[,]にセットしたデータは行と列が入れ替えられ、3,072行50,000列のcolumn majorな配列として扱われています。
こちらのページのEigenを用いた主成分分析のコードと異なり、Eigen側でデフォルトと異なるrow majorな行列として用意したのは、共分散行列を固有値分解して得られた固有ベクトルを格納する行列のみです。
#include "PrincipalComponentAnalysis.h"
using namespace std;
using namespace Eigen;
/**
* Calculate Principal Component Analysis with Eigen (C++ implementation)
*
* - Since Eigen matrix is column-major, m_array_input's rows and columns are swapped from C# interface
*
* @param m_array_input Pointer to an input matrix values (length: rows * columns): column-major matrix (M_input)
* @param columns Number of columns of an input matrix: Number of sample vectors
* @param rows Number of rows of an input matrix: Size of sample vector
* @param v_array_mean_out Pointer to an output mean vector (length: rows): Mean of sample vectors
* @param m_array_cov_out Pointer to an output covariance martix (length: rows * rows): Covariance matrix of sample vectors
* @param v_array_eigenvalues_out Pointer to an output eigenvalues vector (length: rows): Eigenvalues of covariance matrix
* @param m_array_eigenvectors_out Pointer to an output eigenvectors martix (length: rows * rows): Eigenvectors of covariance matrix (row-major)
*/
void solve_principal_component_analysis_with_eigen(double* m_array_input,
const int columns,
const int rows,
double* v_array_mean_out,
double* m_array_cov_out,
double* v_array_eigenvalues_out,
double* m_array_eigenvectors_out)
{
// Map m_array_input to MatrixXd
// - Since Eigen matrix is column-major, rows and columns are swapped from C# interface
// - M_input (column-major) is a transposed matrix of C# m_array_input matrix (row-major)
Map<MatrixXd> M_input(m_array_input, rows, columns);
// Map v_array_mean_out to VectorXd
Map<VectorXd> V_mean(v_array_mean_out, rows);
// Map m_array_cov_out to MatrixXd
Map<MatrixXd> M_cov(m_array_cov_out, rows, rows);
// Map v_array_eigenvalues_out to VectorXd
Map<VectorXd> eigenvalues(v_array_eigenvalues_out, rows);
// Map m_array_eigenvectors_out to MatrixXd
// - Since map m_array_cov_out is row-major, map as a row-major matrix
Map<Matrix<double, Dynamic, Dynamic, RowMajor>> eigenvectors(m_array_eigenvectors_out, rows, rows);
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "M_input is prepared." << std::endl;
std::cout << M_input(0, 0) << ", ..., " << M_input(0, columns - 1) << std::endl;
std::cout << "......" << std::endl;
std::cout << M_input(rows - 1, 0) << ", ..., " << M_input(rows - 1, columns - 1) << std::endl << std::endl;
#endif
// Calculate the mean of sample row vectors
V_mean = M_input.rowwise().mean();
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "V_mean is prepared." << std::endl;
std::cout << V_mean(0) << ", ..., " << V_mean(rows - 1) << std::endl << std::endl;
#endif
// Subtract v_mean.transpose() from each sample row vector
M_input = M_input.colwise() - V_mean;
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "M_input - V_mean is prepared." << std::endl;
std::cout << M_input(0, 0) << ", ..., " << M_input(0, columns - 1) << std::endl;
std::cout << "......" << std::endl;
std::cout << M_input(rows - 1, 0) << ", ..., " << M_input(rows - 1, columns - 1) << std::endl << std::endl;
#endif
// Calculate covariance matrix
// - Ignore the effect of constant multiplication
// - Skip division by N or N - 1 (N is sample size)
M_cov = M_input * M_input.transpose();
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "M_cov is prepared." << std::endl;
std::cout << M_cov(0, 0) << ", ..., " << M_cov(0, rows - 1) << std::endl;
std::cout << "..." << endl;
std::cout << M_cov(rows - 1, 0) << ", ..., " << M_cov(rows - 1, rows - 1) << std::endl << std::endl;
#endif
// ---------------------------------------------------------------
// Calculate the Eigendecomposition of a covariance matrix
// ---------------------------------------------------------------
SelfAdjointEigenSolver<MatrixXd> esolver(M_cov);
eigenvalues = esolver.eigenvalues();
eigenvectors = esolver.eigenvectors();
// Apply reverse() to make the order of eigenvalues decreasing order
eigenvalues = eigenvalues.reverse().eval();
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "eigenvalues" << std::endl;
std::cout << eigenvalues(0) << ", ..., " << eigenvalues(rows - 1) << std::endl << std::endl;
#endif
// Apply reverse() to eigenvectors because the order of eigenvalues are reversed
eigenvectors = eigenvectors.rowwise().reverse().eval();
#ifdef __ENABLE_CONSOLE_TEST_CODES__
std::cout << "eigenvectors" << endl;
std::cout << eigenvectors(0, 0) << ", ..., " << eigenvectors(0, rows - 1) << std::endl;
std::cout << "..." << endl;
std::cout << eigenvectors(rows - 1, 0) << ", ..., " << eigenvectors(rows - 1, rows - 1) << std::endl << std::endl;
#endif
}
2.6. CUDA/Eigen DLLの主成分分析のコードを呼び出すC#のコード
C#側からCUDAとEigenの主成分分析の関数を呼び出すコードは下記のように記述しました。PrincipalComponentAnalysisWithCuda.dllはCUDAとEigenを使用して主成分分析を行うDLLの名前です。最後のパラメータcalculation_methodで、CUDAを使用した関数を実行するかEigenを使用した関数を実行するかを指定しています。
C#からポインタを使用することができるよう、下記のコードのクラス CudaCppDllFunctions は unsafe なクラスとしています。また、WPFアプリケーションのプロパティの設定で、unsafe キーワードを使用したコードをコンパイルできるようにする設定変更を適用しています。
using System.Runtime.InteropServices;
using System.Security;
namespace CifarPrincipalComponentAnalysis.Utilities;
internal static unsafe class CudaCppDllFunctions
{
[DllImport("PrincipalComponentAnalysisWithCuda.dll"), SuppressUnmanagedCodeSecurity]
public static extern void solve_principal_component_analysis([In] double* m_array_input,
int rows,
int columns,
[Out] double* v_array_mean_out,
[Out] double* m_array_cov_out,
[Out] double* v_array_eigenvalues_out,
[Out] double* m_array_eigenvectors_out,
int calculation_method);
}
上記のコードの静的メソッド solve_principal_component_analysis を呼ぶ C# のコードは下記のようになっています。
solve_principal_component_analysisの最後のパラメータをCALCULATE_WITH_CUDAにするかCALCULATE_WITH_EIGENにするかで、主成分分析をCUDAで実行するかEigenで実行するかを切り替えています。
入力データを格納した二次元配列 X_input を用意し、出力データを格納する一次元配列と二次元配列 _vectorMean, X_cov, _vectorEigenvalues, _matrixEigenvectors のメモリー領域を確保してから CudaCppDllFunctions.solve_principal_component_analysis メソッドを呼んでいます。
C#の一次元配列と二次元配列をポインタで渡すため、unsafe ブロックを用意し、その中で fixed を使用しています。
double[,]? X_input = new double[numberOfImages, ImageDataSize];
for (int row = 0; row < numberOfImages; row++)
{
for (int column_i = 0; column_i < ImageAreaSize; column_i++)
{
X_input[row, 3 * column_i] = (double) _dataImages[row].BlueChannelData[column_i]; // blue
X_input[row, 3 * column_i + 1] = (double) _dataImages[row].GreenChannelData[column_i]; // green
X_input[row, 3 * column_i + 2] = (double) _dataImages[row].RedChannelData[column_i]; // red
}
}
double[,]? X_cov;
#if PCA_WITH_CUDA
//
// Use CUDA (cuBLAS and cuSOLVER) to calculate PCA
//
_vectorMean = new double[ImageDataSize];
X_cov = new double[ImageDataSize, ImageDataSize];
_vectorEigenvalues = new double[ImageDataSize];
_matrixEigenvectors = new double[ImageDataSize, ImageDataSize];
unsafe
{
fixed (double* m_array_input = X_input,
v_array_mean_out = _vectorMean,
m_array_cov_out = X_cov,
v_array_eigenvalues_out = _vectorEigenvalues,
m_array_eigenvectors_out = _matrixEigenvectors)
{
CudaCppDllFunctions.solve_principal_component_analysis(m_array_input,
numberOfImages,
ImageDataSize,
v_array_mean_out,
m_array_cov_out,
v_array_eigenvalues_out,
m_array_eigenvectors_out,
CALCULATE_WITH_CUDA);
}
}
#elif PCA_WITH_EIGEN
//
// Use Eigen to calculate PCA
//
_vectorMean = new double[ImageDataSize];
X_cov = new double[ImageDataSize, ImageDataSize];
_vectorEigenvalues = new double[ImageDataSize];
_matrixEigenvectors = new double[ImageDataSize, ImageDataSize];
unsafe
{
fixed (double* m_array_input = X_input,
v_array_mean_out = _vectorMean,
m_array_cov_out = X_cov,
v_array_eigenvalues_out = _vectorEigenvalues,
m_array_eigenvectors_out = _matrixEigenvectors)
{
CudaCppDllFunctions.solve_principal_component_analysis(m_array_input,
numberOfImages,
ImageDataSize,
v_array_mean_out,
m_array_cov_out,
v_array_eigenvalues_out,
m_array_eigenvectors_out,
CALCULATE_WITH_EIGEN);
}
}
#else
2.7. 動作確認
Releaseビルドを選択して、WPFアプリケーションとCUDA C/C++のDLLの2つのプロジェクトをビルドします。
その後、Git Bash で CifarPrincipalComponentAnalysisWithCuda/bin/Release/net8.0-windows ディレクトリに移動し、下記のコマンドを実行して CifarPrincipalComponentAnalysisWithCuda.exe を起動します。
$ ./CifarPrincipalComponentAnalysisWithCuda.exe
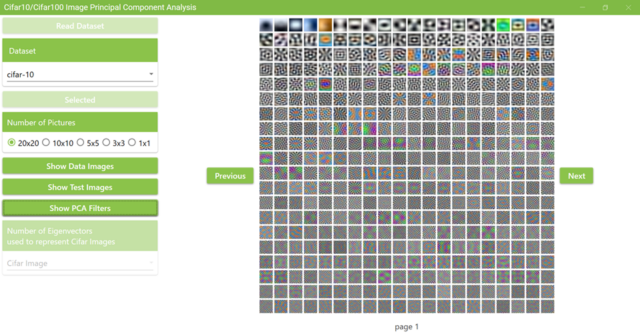
アプリケーション起動後、こちらのページと同様の手順で Cifar10 または Cifar100 のデータを読み取ります。その後、「Show PCA Filters」ボタンをクリックすると下の画像のようなメッセージボックスが表示されるので、「OK」をクリックします。
一度主成分分析を実行すると、その後は計算済みの主成分分析の結果のデータを使用することになります。主成分分析の結果のデータはCifar10とCifar100のデータを格納したディレクトリに保存されます。主成分分析の結果のデータを削除して「Show PCA Filters」ボタンをクリックすると、主成分分析の計算がまた実行されます。
Git Bash から CifarPrincipalComponentAnalysisWithCuda.exe を起動して主成分分析を実行すると、下記のようなログがコンソールに出力されます。下記のログは__ENABLE_CONSOLE_TEST_CODES__を有効にし、主成分分析の計算結果の確認コードを実行し、コンソールに出力するようにした場合のログになります。CUDAとEigenで計算した場合のログと主成分ベクトルを可視化した画像を順に並べました。
CUDAで計算した場合のログ (__ENABLE_CONSOLE_TEST_CODES__は有効)
fukagai@ESPRIMO_WD2H2 MINGW64 /c/repos/cifar10-cifar100-principal-component-analysis-with-cuda/CifarPrincipalComponentAnalysisWithCuda/bin/Release/net8.0-windows (main) $ ./CifarPrincipalComponentAnalysisWithCuda.exe PCA calculation is started. --- C++ codes (START) --- --- solve_principal_component_analysis (START) --- M_input: 63, ..., 239 M_input: ...... M_input: 123, ..., 163 V_mean: 132.554, ..., 126.639 M_input - V_mean: -69.5538, ..., 106.446 M_input - V_mean: ...... M_input - V_mean: -3.63908, ..., 36.3609 cusolverDnXsyevd_bufferSize: workspaceInBytesOnDevice = 226726024 cusolverDnXsyevd_bufferSize: workspaceInBytesOnHost = 0 after Xsyevd: info = 0 M_cov is prepared. 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 eigenvalues 1.79996e+11, ..., 5160.25 eigenvectors 0.0311112, ..., 0.0018612 ... 0.015737, ..., -0.00511573 Check Result: M_cov * V 5.5999e+09, ..., 9.60427 ... 2.83261e+09, ..., -26.3985 Check Result: V * L 5.5999e+09, ..., 9.60427 ... 2.83261e+09, ..., -26.3985 Check Result: V V^t 1, ..., -6.9931e-17 ... -6.9931e-17, ..., 1 Check Result: V L V^t 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 --- solve_principal_component_analysis (END) --- --- C++ codes (END) --- PCA calculation processing time is 00:00:29.1973187
得られた主成分ベクトルを第一主成分から順に400番目まで並べて可視化した画像
Eigenで計算した場合のログ (__ENABLE_CONSOLE_TEST_CODES__は有効)
fukagai@ESPRIMO_WD2H2 MINGW64 /c/repos/cifar10-cifar100-principal-component-analysis-with-cuda/CifarPrincipalComponentAnalysisWithCuda/bin/Release/net8.0-windows (main) $ ./CifarPrincipalComponentAnalysisWithCuda.exe PCA calculation is started. --- C++ codes (START) --- --- solve_principal_component_analysis (START) --- M_input is prepared. 63, ..., 239 ...... 123, ..., 163 V_mean is prepared. 132.554, ..., 126.639 M_input - V_mean is prepared. -69.5538, ..., 106.446 ...... -3.63908, ..., 36.3609 M_cov is prepared. 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 eigenvalues 1.79996e+11, ..., 5160.25 eigenvectors 0.0311112, ..., -0.0018612 ... 0.015737, ..., 0.00511573 M_cov is prepared. 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 eigenvalues 1.79996e+11, ..., 5160.25 eigenvectors 0.0311112, ..., -0.0018612 ... 0.015737, ..., 0.00511573 Check Result: M_cov * V 5.5999e+09, ..., -9.60427 ... 2.83261e+09, ..., 26.3985 Check Result: V * L 5.5999e+09, ..., -9.60427 ... 2.83261e+09, ..., 26.3985 Check Result: V V^t 1, ..., -8.32017e-16 ... -8.32017e-16, ..., 1 Check Result: V L V^t 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 --- solve_principal_component_analysis (END) --- --- C++ codes (END) --- PCA calculation processing time is 00:02:10.3043911
得られた主成分ベクトルを第一主成分から順に400番目まで並べて可視化した画像
CUDAとEigenで計算した主成分ベクトルを可視化した画像には違いがあります。これは主成分ベクトルの中に、CUDAとEigenの計算結果で向きが反対方向となるベクトルが含まれているためです。
上記のログのハイライトした行は、主成分ベクトルを並べた行列の途中を省略した4つの角の値を示しています。主成分ベクトルは大きな固有値に対応する主成分ベクトルから順に、1列目から順に並んでいます。1列目の主成分ベクトルは方向が同じですが、3,072列目の主成分ベクトルは向きが反対方向になっています。このように反対方向を向いたベクトルが存在するため、得られた主成分ベクトルを可視化した画像に違いが出ています。
また、__ENABLE_CONSOLE_TEST_CODES__を有効にして確認用の行列計算を実行しているため、ログに出力される計算時間は__ENABLE_CONSOLE_TEST_CODES__を無効にしたときよりも長くなっています。
3. 計算時間
デスクトップパソコンESPRIMO WD2/H2でCifar10のtrainingデータを入力として主成分分析を実行したときの条件と計算時間を表にまとめました。計算時間は__ENABLE_CONSOLE_TEST_CODES__を無効にして確認しました。
| デスクトップパソコン | ESPRIMO WD2/H2 | |
| プロセッサ | 13th Gen Intel(R) Core(TM) i5-13400 2.50 GHz | |
| GPGPU | NVIDIA GeForce GTX 1650 | |
| 実装 RAM | 16.0 GB (15.2 GB 使用可能) | |
| システムの種類 | 64 ビット オペレーティング システム、x64 ベース プロセッサ | |
| エディション | Windows 11 Pro | |
| バージョン | 23H2 | |
| OS ビルド | 22631.3374 | |
| TargetFramework | net8.0-windows | |
| Eigen 3.4.0を使用した 主成分分析の計算 |
共分散行列を計算後、SelfAdjointEigenSolverで固有値分解を実行 | 計算時間:1分54.84秒 |
| CUDA Toolkit 12.4を使用した 主成分分析の計算 |
cuBLAS, cuSOLVER, thrustで主成分分析の計算を実行 | 計算時間:12.01秒 |