Cifar10/Cifar100の画像データセットをC#で主成分分析 (C++のEigenを利用)
1. 概要
以前、Cifar10/Cifar100の画像データセットを主成分分析するC#のプログラムを作成し、こちらのページに説明を記載しました。
主成分分析の計算にはC#のAccord.NETを使用し、共分散行列をAccord.NETのSingularValueDecompositionで特異値分解しました。私のノートパソコンLifebook WU2/D2(型名 FMVWD2U27)で2時間ほどの計算時間を要しました。
この計算を高速化するため、C#でAccord.NETを使用して実行していた主成分分析の計算を、C++でEigenを使用して実行するようにしました。共分散行列を求めた後、対称行列の固有値分解を実行するSelfAdjointEigenSolverを使用して固有値分解するようにしました。主成分分析の計算時間は約2分30秒ほどに短縮されました。
C#の主成分分析の計算も少し修正し、共分散行列をAccord.NETのEigenvalueDecompositionで固有値分解するようにしました。C++でEigenを使用して計算したときよりは計算時間を要しましたが、特異値分解で計算していたときよりも計算時間は短縮され、約40分で計算できるようになりました。
ソースコードは下記のGitHubリポジトリに置きました。
https://github.com/fukagai-takuya/cifar10-cifar100-principal-component-analysis-with-eigen/
2. 実装方法
2.1. Eigenのダウンロード
Git Bashで下記のコマンドを実行し、C:\dev\eigenにEigenをダウンロードしました。
$ cd /c/dev/ $ git clone https://gitlab.com/libeigen/eigen.git
2.2. C++のEigenを使用するDLLの作成
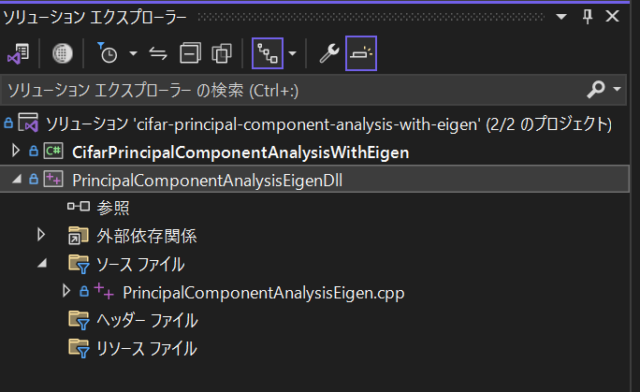
以前、Visual Studio 2022で作成したCifar10/Cifar100の画像データセットをC#で主成分分析するWPFアプリケーションのソリューションにC++のDLLを作成するプロジェクトを追加しました。
追加後のソリューションは、WPFアプリケーションとC++のDLLの2つのプロジェクトからなるソリューションです。
WPFアプリケーションのターゲットOSを「Windows」、ターゲットOSバージョンを「7.0」に設定しました。また、必ずしもそうする必要はありませんが、ターゲットフレームワークを「.NET 6.0」から「.NET 8.0」に変更しました。
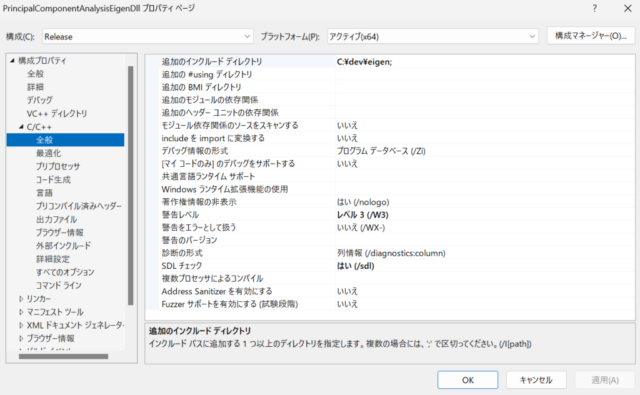
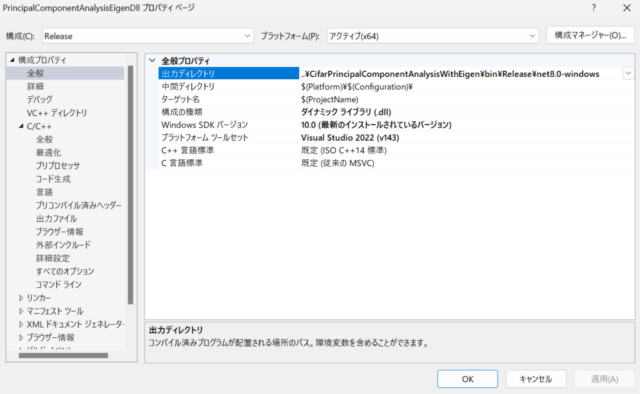
C++のDLLを作成するプロジェクトのプロパティからReleaseビルドを選択し、下の中央の画像のように「追加のインクルードディレクトリ」を「C:\dev\eigen;」に設定しました。また、下の右の画像のようにC++のDLLの出力先ディレクトリをReleaseビルドしたWPFアプリケーションの実行ファイルが出力されるディレクトリに変更しました。プリコンパイル済みヘッダーを使用しないようにしたため、プロジェクトのプロパティで「プリコンパイル済みヘッダーを使用しない」を選択する設定変更も適用しています。
2.3. C++のEigenを使った主成分分析の計算
C++のDLLのプロジェクトには下記のようなC++のコードを記載したファイル PrincipalComponentAnalysisEigen.cpp を追加しました。
関数 solve_principal_component_analysis はC#のコードから呼び出される関数で、関数宣言の前に extern “C” __declspec(dllexport) を追加するようにしています。#define 文で DLLEXPORT を定義して追加するようにしています。
関数 solve_principal_component_analysis は入力となるデータを行数 rows、列数 columns の二次元配列 (m_array_input) で受け取ります。この二次元配列の行数はサンプルデータ数、列数はサンプルデータベクトルのサイズです。
この関数は、入力サンプルデータの平均ベクトル (v_array_mean_out)、共分散行列 (m_array_cov_out)、共分散行列の固有値を降順に並べたベクトル (v_array_eigenvalues_out)、共分散行列の固有ベクトル (列ベクトル) を対応する固有値の順に左から並べた行列 (m_array_eigenvectors_out) を返します。
下記のコードのコメントに書いたようにC#の二次元配列のデータ順は Row Major ですが、Eigen の Matrix はデフォルトでは Column Major なため、Row Major な Matrix にデータをマップするよう指定しています。出力用の二次元配列についても同様です。
固有値分解を実行する SelfAdjointEigenSolver の解の固有値の配列は eigenvalues() で取得できます。取得した固有値は昇順に並んでいますが、ここでは降順に並んだ固有値を取得したいので reverse() で順序を反転させています。固有ベクトルも同様で、固有ベクトル (列ベクトル) が左の列から順に並んだ行列を eigenvectors() で取得した後、 rowwise().reverse() で固有値の順に合わせて反転させています。列ベクトルとして並んだ固有ベクトルの行方向の順序を反転させる操作になります。
下記のコードには、実行結果に問題がないか確認し、コンソールに結果を出力するコードも含まれています。
#define DLLEXPORT extern "C" __declspec(dllexport)
#include <iostream>
#include <Eigen/Core>
#include <Eigen/Eigenvalues>
using namespace std;
using namespace Eigen;
DLLEXPORT void solve_principal_component_analysis(double* m_array_input,
const int rows,
const int columns,
double* v_array_mean_out,
double* m_array_cov_out,
double* v_array_eigenvalues_out,
double* m_array_eigenvectors_out)
{
cout << "--- C++ codes (START) ---" << endl;
cout << "--- solve_principal_component_analysis (START) ---" << endl;
// Map m_array_input to MatrixXd
// rows: Number of sample row vectors
// columns: Size of sample row vectors
// - Make memory array Row Major to map m_array_input (Eigen's default order is Column Major)
// - C# two dimensional array double[,] is Row Major
Map<Matrix<double, Dynamic, Dynamic, RowMajor>> m_input(m_array_input, rows, columns);
cout << "m_input is prepared." << endl;
// ---------------------------------------------------------------
// Calculation of Covariance Matrix
// ---------------------------------------------------------------
// Map v_array_mean_out to VectorXd
// - The size of mean vector is columns
Map<VectorXd> v_mean(v_array_mean_out, columns);
// Calculate the mean of sample row vectors
v_mean = m_input.colwise().mean();
cout << "v_mean" << endl;
cout << v_mean(0) << ", ..., " << v_mean(columns - 1) << endl << endl;
// Subtract v_mean.transpose() from each sample row vector
m_input = m_input.rowwise() - v_mean.transpose();
// Map m_array_cov_out to MatrixXd
// - The size of rows and columns are the same as the input sample row vectors
// - Make memory array Row Major to map m_array_cov_out
Map<Matrix<double, Dynamic, Dynamic, RowMajor>> m_cov(m_array_cov_out, columns, columns);
// Calculate covariance matrix
// - Ignore the effect of constant multiplication
// - Skip division by N or N - 1 (N is sample size)
m_cov = m_input.adjoint() * m_input;
cout << "m_cov is prepared." << endl;
cout << m_cov(0, 0) << ", ..., " << m_cov(0, columns - 1) << endl;
cout << "..." << endl;
cout << m_cov(columns - 1, 0) << ", ..., " << m_cov(columns - 1, columns - 1) << endl << endl;
// ---------------------------------------------------------------
// Calculate Eigendecomposition of a covariance matrix
// ---------------------------------------------------------------
SelfAdjointEigenSolver<MatrixXd> esolver(m_cov);
// Map v_array_eigenvalues_out to VectorXd
Map<VectorXd> eigenvalues(v_array_eigenvalues_out, columns);
// Apply reverse() to make the order of eigenvalues decreasing order
eigenvalues = esolver.eigenvalues().reverse().eval();
cout << "eigenvalues" << endl;
cout << eigenvalues(0) << ", ..., " << eigenvalues(columns - 1) << endl << endl;
// Map m_array_eigenvectors_out to MatrixXd
// - Make memory array Row Major to map m_array_cov_out
Map<Matrix<double, Dynamic, Dynamic, RowMajor>> eigenvectors(m_array_eigenvectors_out, columns, columns);
// Apply reverse() to eigenvectors because the order of eigenvalues are reversed
eigenvectors = esolver.eigenvectors().rowwise().reverse().eval();
cout << "eigenvectors" << endl;
cout << eigenvectors(0, 0) << ", ..., " << eigenvectors(0, columns - 1) << endl;
cout << "..." << endl;
cout << eigenvectors(columns - 1, 0) << ", ..., " << eigenvectors(columns - 1, columns - 1) << endl << endl;
cout << "Check Result: P L P^t" << endl;
MatrixXd PLPt = eigenvectors * eigenvalues.asDiagonal() * eigenvectors.transpose();
cout << PLPt(0, 0) << ", ..., " << PLPt(0, columns - 1) << endl;
cout << "..." << endl;
cout << PLPt(columns - 1, 0) << ", ..., " << PLPt(columns - 1, columns - 1) << endl << endl;
cout << "--- solve_principal_component_analysis (END) ---" << endl;
cout << "--- C++ codes (END) ---" << endl;
}
2.4. C++の主成分分析のコードを呼び出すC#のコード
WPFアプリケーションのプロジェクトに下記の内容のファイル Utilities/EigenCppDllFunctions.cs を用意し、C++のDLLの関数 solve_principal_component_analysis を呼ぶようにしました。下記のコードの PrincipalComponentAnalysisEigenDll.dll は 2.2.で追加したプロジェクトが生成するC++のDLLの名前です。2.2.の設定で、このDLLはWPFアプリケーションの実行ファイルと同じディレクトリに出力されるようにしています。
C#からポインタを使用することができるよう、下記のコードのクラス EigenCppDllFunctions は unsafe なクラスとしています。また、WPFアプリケーションのプロパティの設定で、unsafe キーワードを使用したコードをコンパイルできるようにする設定変更を適用しました。
using System.Runtime.InteropServices;
using System.Security;
namespace CifarPrincipalComponentAnalysis.Utilities;
internal static unsafe class EigenCppDllFunctions
{
[DllImport("PrincipalComponentAnalysisEigenDll.dll"), SuppressUnmanagedCodeSecurity]
public static extern void solve_principal_component_analysis([In] double* m_array_input,
int rows,
int columns,
[Out] double* v_array_mean_out,
[Out] double* m_array_cov_out,
[Out] double* v_array_eigenvalues_out,
[Out] double* m_array_eigenvectors_out);
}
上記のコードの静的メソッド solve_principal_component_analysis を呼ぶ C# のコードは下記のようになっています。
入力データを格納した二次元配列 X_input を用意し、出力データを格納する一次元配列と二次元配列 _vectorMean, X_cov, _vectorEigenvalues, _matrixEigenvectors のメモリー領域を確保してから EigenCppDllFunctions.solve_principal_component_analysis メソッドを呼んでいます。
C#の一次元配列と二次元配列をポインタで渡すため、unsafe ブロックを用意し、その中で fixed を使用しています。
double[,]? X_input = new double[numberOfImages, ImageDataSize];
for (int row = 0; row < numberOfImages; row++)
{
for (int column_i = 0; column_i < ImageAreaSize; column_i++)
{
X_input[row, 3 * column_i] = (double) _dataImages[row].BlueChannelData[column_i]; // blue
X_input[row, 3 * column_i + 1] = (double) _dataImages[row].GreenChannelData[column_i]; // green
X_input[row, 3 * column_i + 2] = (double) _dataImages[row].RedChannelData[column_i]; // red
}
}
double[,]? X_cov;
#if USE_EIGEN
//
// Use Eigen (C++ library) to calculate PCA
//
_vectorMean = new double[ImageDataSize];
X_cov = new double[ImageDataSize, ImageDataSize];
_vectorEigenvalues = new double[ImageDataSize];
_matrixEigenvectors = new double[ImageDataSize, ImageDataSize];
unsafe
{
fixed (double* m_array_input = X_input,
v_array_mean_out = _vectorMean,
m_array_cov_out = X_cov,
v_array_eigenvalues_out = _vectorEigenvalues,
m_array_eigenvectors_out = _matrixEigenvectors)
{
EigenCppDllFunctions.solve_principal_component_analysis(m_array_input,
numberOfImages,
ImageDataSize,
v_array_mean_out,
m_array_cov_out,
v_array_eigenvalues_out,
m_array_eigenvectors_out);
}
}
#else
2.5. C++のDLLを使用しない場合
ファイル Models/CifarDataset.cs で下記のコードのように USE_EIGEN を定義しています。この状態でビルドするとC++のEigenを使用するプログラムがビルドされます。
#define USE_EIGEN
下記のようにコメントアウトしてビルドすると Accord.NET の EigenvalueDecomposition を使用するプログラムがビルドされます。
//#define USE_EIGEN
2.6. 動作確認
Releaseビルドを選択して、WPFアプリケーションとC++のDLLの2つのプロジェクトをビルドします。
その後、Git Bash で CifarPrincipalComponentAnalysisWithEigen/bin/Release/net8.0-windows ディレクトリに移動し、下記のコマンドを実行して CifarPrincipalComponentAnalysisWithEigen.exe を起動します。
$ ./CifarPrincipalComponentAnalysisWithEigen.exe
アプリケーション起動後、こちらのページと同様の手順で Cifar10 または Cifar100 のデータを読み取ります。その後、「Show PCA Filters」ボタンをクリックすると下の画像のようなメッセージボックスが表示されるので、「OK」をクリックします。
一度主成分分析を実行すると、その後は計算済みの主成分分析の結果のデータを使用することになります。主成分分析の結果のデータはCifar10とCifar100のデータを格納したディレクトリに保存されます。主成分分析の結果のデータを削除して「Show PCA Filters」ボタンをクリックすると、主成分分析の計算がまた実行されます。
Git Bash から CifarPrincipalComponentAnalysisWithEigen.exe を起動して主成分分析を実行すると、下記のようなログがコンソールに出力されます。ログには主成分分析の実行時間の測定結果も含まれています。
$ ./CifarPrincipalComponentAnalysisWithEigen.exe PCA calculation is started. --- C++ codes (START) --- --- solve_principal_component_analysis (START) --- m_input is prepared. v_mean 132.554, ..., 126.639 m_cov is prepared. 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 eigenvalues 1.79996e+11, ..., 5160.25 eigenvectors 0.0311112, ..., -0.0018612 ... 0.015737, ..., 0.00511573 Check Result: P L P^t 3.23602e+08, ..., 6.66941e+07 ... 6.66941e+07, ..., 2.10767e+08 --- solve_principal_component_analysis (END) --- --- C++ codes (END) --- PCA calculation processing time is 00:01:53.9159126 _vectorMean: 132.5538, ..., 126.63908 X_cov: 323601651.2779998, ..., 66694125.874800056 ... X_cov: 66694125.874800056, ..., 210766896.83767992 _vectorEigenvalues: 179996402559.84167, ..., 5160.249723685157 _matrixEigenvectors: 0.03111119420487357, ..., -0.001861201694741981 ... _matrixEigenvectors: 0.015737041116741294, ..., 0.005115732425291488 P^T P: 1.0000000000000042, ..., -1.5368565794982025E-17 ... P^T P: -1.5368565794982025E-17, ..., 1.000000000000006 PLP^T: 323601651.27801186, ..., 66694125.87479978 ... PLP^T: 66694125.87479978, ..., 210766896.83769244
3. 計算時間
私のノートパソコンLifebook WU2/D2(型名 FMVWD2U27)とデスクトップパソコンESPRIMO WD2/H2でCifar10のtrainingデータを入力として主成分分析を実行したときの条件と計算時間を表にまとめました。
| ノートパソコン | Lifebook WU2/D2(型名 FMVWD2U27) | |
| プロセッサ | Intel(R) Core(TM) i3-8145U CPU @ 2.10GHz 2.30 GHz | |
| 実装 RAM | 8.00 GB (7.75 GB 使用可能) | |
| システムの種類 | 64 ビット オペレーティング システム、x64 ベース プロセッサ | |
| エディション | Windows 11 Home | |
| バージョン | 22H2 | |
| OS ビルド | 22621.3155 | |
| TargetFramework | net8.0-windows | |
| Accord.Math 3.8.0を使用した 主成分分析の計算 |
共分散行列を計算後、EigenvalueDecompositionで固有値分解を実行 | 計算時間:39分19秒 |
| Eigen 3.4.0を使用した 主成分分析の計算 |
共分散行列を計算後、SelfAdjointEigenSolverで固有値分解を実行 | 計算時間:2分34秒 |
| デスクトップパソコン | ESPRIMO WD2/H2 | |
| プロセッサ | 13th Gen Intel(R) Core(TM) i5-13400 2.50 GHz | |
| 実装 RAM | 16.0 GB (15.2 GB 使用可能) | |
| システムの種類 | 64 ビット オペレーティング システム、x64 ベース プロセッサ | |
| エディション | Windows 11 Pro | |
| バージョン | 23H2 | |
| OS ビルド | 22631.3155 | |
| TargetFramework | net8.0-windows | |
| Accord.Math 3.8.0を使用した 主成分分析の計算 |
共分散行列を計算後、EigenvalueDecompositionで固有値分解を実行 | 計算時間:23分32秒 |
| Eigen 3.4.0を使用した 主成分分析の計算 |
共分散行列を計算後、SelfAdjointEigenSolverで固有値分解を実行 | 計算時間:1分54秒 |